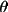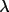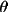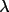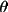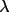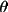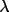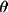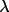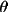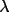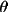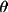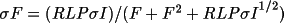|
| Lorentz factor | = 1/(2sin 2
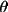 ) ) |
for single crystal |
= 1/(2sin 2
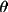 sin sin
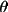 ) ) |
for powder |
The formulae used for polarization are those described by Azaroff (1955), Hope (1971), and Vincent & Flack (1980). The general expression for polarization of a twice-diffracted beam is
P =
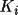 (1-B)(
(1-B)(
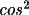
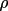
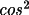 2
2
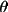 +
+
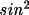
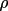 ) + B(
) + B(
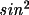
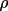
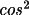 2
2
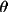 +
+
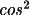
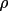 ) / [(1-B)
) / [(1-B)
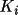 +B]
+B]
where
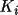 , the polarization ratio
is
, the polarization ratio
is
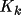 =
=
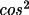 2
2
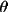
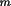 for an ideal mozaic crystal and
for an ideal mozaic crystal and
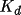 = |cos 2
= |cos 2
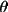
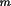 | for an ideal crystal. B is the fraction of the
intensity with the electric field parallel to the plane
of the monochromator (Azaroff's notation is
| for an ideal crystal. B is the fraction of the
intensity with the electric field parallel to the plane
of the monochromator (Azaroff's notation is
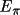 ). This direction
is given by the cross product of the vector in the
direction of the source beam and the normal to the
monochromator crystal plane. In a standard X-ray
diffractometer the source beam is unpolarized and B=0.5.
). This direction
is given by the cross product of the vector in the
direction of the source beam and the normal to the
monochromator crystal plane. In a standard X-ray
diffractometer the source beam is unpolarized and B=0.5.
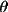
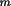 is the monochromator angle and
is the monochromator angle and
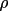 is the angle
between 2 planes of diffraction (i.e. planes, containing
the incident and reflected rays of the monochromator and
the sample).
is the angle
between 2 planes of diffraction (i.e. planes, containing
the incident and reflected rays of the monochromator and
the sample).
The general expression for the integrated polarization of mosaic/perfect crystal is
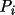 = (1-C)
= (1-C)
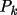 + C
+ C
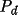 .
.
where C is the monochromator perfection factor (the
fraction of the monochromator crystal considered to be
perfect) and
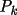 and
and
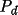 the kinematic and
dynamical components of the polarization.
RLP is the reciprocal of
Lp.
the kinematic and
dynamical components of the polarization.
RLP is the reciprocal of
Lp.
X-ray powder, no monochromator
RLP1 = 2sin
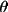 sin 2
sin 2
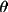 / (1 +
/ (1 +
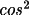 2
2
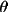 )
)
X-ray single crystal, no monochromator
RLP2 = 2sin 2
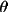 / (1 +
/ (1 +
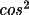 2
2
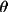 )
)
X-ray single crystal, with monochromator and perfection factor, perpendicular setting
In the perpendicular monochromator setting, the
rotation axis of the monochromator crystal is
perpendicular to the normal to the equatorial plane of
the diffractometer (ie. 2
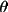 axis), such that
the plane of the incident beam and the beam reflected by
the monochromator is perpendicular to the plane of the
beam reflected by the monochromator and the beam
reflected by the crystal under study. Rho, as defined by
Azaroff, is 90°. If the source beam incident on the
monochromator is unpolarized then B=0.5. For a perfectly
polarized beam B=0. for this setting.
This is the CAD4 setting.
axis), such that
the plane of the incident beam and the beam reflected by
the monochromator is perpendicular to the plane of the
beam reflected by the monochromator and the beam
reflected by the crystal under study. Rho, as defined by
Azaroff, is 90°. If the source beam incident on the
monochromator is unpolarized then B=0.5. For a perfectly
polarized beam B=0. for this setting.
This is the CAD4 setting.
T1 = (1 - C) ((1-B)
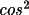 2
2
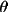
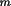 +
+
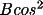 2
2
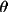 ) / (B +(1-B)
) / (B +(1-B)
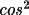 2
2
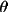
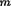 )
)
T2 = C(
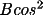 2
2
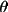 + (1-B)cos2
+ (1-B)cos2
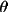
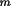 ) / (B + (1-B)cos2
) / (B + (1-B)cos2
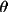
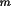 )
)
RLP3 = sin2
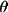 / (T1 +
T2)
/ (T1 +
T2)
X-ray single crystal, with monochromator and perfection factor, parallel setting
For the equatorial, or normal, monochromator
setting, the rotation axis of the monochromator is
parallel to the normal to the equatorial plane of the
diffractometer (ie. 2
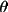 axis) such that
the incident beam, the beam reflected by the
monochromator and the beam reflected by the crystal under
study all lie in the same plane. If the source beam
incident on the monochromator is unpolarized then B=0.5.
For a perfectly polarized beam B=1. for this setting.
This is the Nicolet setting.
axis) such that
the incident beam, the beam reflected by the
monochromator and the beam reflected by the crystal under
study all lie in the same plane. If the source beam
incident on the monochromator is unpolarized then B=0.5.
For a perfectly polarized beam B=1. for this setting.
This is the Nicolet setting.
T1 = (1 - C) (B + (1-B)
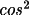 2
2
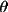
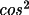 2
2
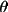
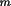 ) / (B + (1-B)
) / (B + (1-B)
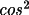 2
2
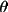
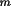 )
)
T2 = C(B + (1-B)
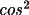 2
2
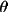 cos2
cos2
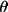
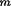 ) / (B + (1-B)cos2
) / (B + (1-B)cos2
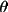
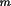 )
)
RLP4 = sin2
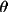 / (T1 +
T2)
/ (T1 +
T2)
Neutron powder (no polarization)
RLP1 = 2sin
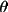 sin 2
sin 2
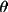
Neutron single crystal
RLP2 = 2sin 2
-
Reads
lrcell:and symmetry data from the input archive bdf -
Writes updated file to the output archive bdf
-
Optionally, reads reflection data form specified (on bdfin ) bdf
title CREATION OF AB INITIO REFLECTION RECORD ADDREF dset 1 ffac list reduce itof rlp2 hklin skip hkl rcod irel sigi absf eval remove irel sigi hkl p6122 0 1 1 1 22004.8 4043.4 1.0 3.0 hkl p6122 0 1 4 1 387.4 205.5 1.0 1.0 hkl p6122 0 1 5 1 6735.0 1110.5 1.0 3.0 :...................................reflection data omitted for brevity hkl p6122 2 2 7 1 358.1 98.2 1.0 0.3 hkl p6122 2 2 8 1 384.3 78.1 1.0 0.3 hkl p6122 2 3 3 1 2275.6 247.0 1.0 2.0
The ADDREF line specifies that interpolated form
factors are to be inserted in
lrrefl:
, and that all reflections are to be listed. The
reduce line indicates
that relative intensities and their sigmas are to be
converted to relative F's and
 (F)'s; the Lp
factor is to be calculated by method 2 (spectrometer with
Eulerian cradle geometry and 2
(F)'s; the Lp
factor is to be calculated by method 2 (spectrometer with
Eulerian cradle geometry and 2
 scan). The
hklin line specifies the
items which are found on
hkl lines. Note that the
user has labeled the
hkl lines with the
compound identification, so
scan). The
hklin line specifies the
items which are found on
hkl lines. Note that the
user has labeled the
hkl lines with the
compound identification, so
must be used to ignore this data. The
remove line indicates
that
skip
and
irel
are to be excluded from the output bdf (they
are used, however, in the conversion to
sigi
and
frel
, so they must be specified on the
hklin and
hkl lines.
sigf
title Contraction of the reflection record ADDREF bdfin all remove absf tbar extf
To decrease the size of a large archive
bdf, first check to see which items are in
lrrefl:
of the file. Then check (carefully) to see which
items are no longer necessary to keep in the bdf. Use the
remove line to get rid of
these, as in the procedure above. The input archive bdf is
read. The absorption correction, extinction correction, and
mean radiation path length will be removed from
lrrefl:
of the bdf by the lines above.
title Merging of reflection data ADDREF bdfin file a all bdfin file ddd absf eval
Suppose the input archive bdf contains
reflection information about a compound and the bdf with
extension
DDDcontains a bdf with
different reflection information about the same compound.
The preceding sequence of lines will merge certain items
from both bdf's and output them to the output archive bdf.
title EXAMPLE USE OF CONTINUATION LINES ADDREF dset 1 hklin hkl frel sigf fcal 1000 1001 1002 c 1003 rcod tbar hkl 1 1 1 40 5 56 289 33 256 4 0.1
The preceding example illustrates the use of c lines. Note that some items are specified using ID numbers and some are specified using four-letter mnemonics.
title Generate reflection data to sin(theta)/lambda=.5 ADDREF limits *4 0.5 hklgen hkl frel title Complete data preparation sequence STARTX cell 11.52 11.21 4.92 90 90.833 90 288.0 cellsd .012 .011 .005 0.0 .0005 0.0 sgname -p 2yab :p21/a celcon o 12 celcon c 28 celcon h 24 DIFDAT cad attenu 5. genscl 3 SORTRF order khl aver 1 cull 1.5 print 1500 pakfrl ADDREF dset 1 list 7 ffac lpin friedel reduce itof rlp2 xray bdfin hkl irel sigi rcod ifri sfri rcdf remove irel sigi ifri sfri
In this example a run of
STARTX
,
DIFDAT
,
SORTRF
, and ADDREF is combined to produce a bdf with F
values in logical record
lrrefl:
for a unique asymmetric set of reflections
including the Friedel related pairs.
-
Azaroff, L.V. 1955. Polarization Correction for Crystal-MonochromatizedX-radiation. Acta Cryst. 8, 701.
-
Hope, H. 1977. Polarization Factor for Graphite X-ray Monochrometers. Acta Cryst. A27, 392.
-
Iwasaki, Hitoshi and Ito, Tetsuzo. 1977. Values of Epsilon for Obtaining Normalized Structure Factors . Acta Cryst. A33, 227-229.
-
Karle, I. 1969. General Procedure for Phase Determination. Crystallographic Computing. F.R. Ahmed, Sydney R. Hall, C.P. Huber, eds., Munksgaard. Copenhagen:19-25.
-
Kasper, John S. and Lonsdale, Kathleen. 1959. Eds. International Tables for X-ray Crystallography Vol. II. Birmingham, England: Kynoch Press.
-
Larson, A.C. 1969. The Inclusion of Secondary Extinction in Least-Squares Refinement of Crystal Structures. Crystallographic Computing.
-
F.R. Ahmed, S.R.Hall, C.P.Huber, eds., Munksgaard. Copenhagen: 291-294. Rollett, J.S. 1965. Computing Techniques in Crystallography. Elmsford, NY: Pergamon Press.
-
Stewart, J.M. and Karle, J. 1976. The Calculation of Epsilon Associated with Normalized Structure Factors, E. Acta Cryst. A32, 1005-1007.
-
Stewart, J.M. and Karle, J. 1977. Two Papers on the Calculation of Epsilon for Obtaining Normalized Structure Factors. Acta Cryst. A33, 519.
-
Vincent, M.G. and Flack, H.D. 1980. On the Polarization Factor for Crystal Monochromated X-radiation I Assessment of Errors. Acta Cryst. A36,610.