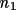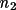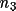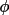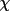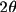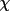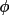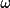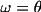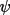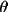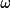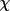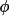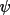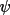|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| System | Senses of Rotation | ||||
2
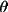 |
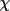
|
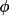
|
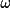
|
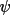 [a]
[a]
|
|
| Siemens (Syntex, Nicolet) | A | A | C | A | |
| CAD-4 | C | C | C | C | |
| Philips PW 1100 | A | C | A | A | C |
| Busing and Levy (1967) | C | C | C | C | C |
| Chidambaram (1980) | A | A | A | A | |
| International Tables, Vol. IV | C | A | A | A | A |
| Picker FACS-1 | C | A | A | C | |
| Picker with Finger refinement | C | C | C | C | |
[a] At the present time the ABSORB program
does not handle any system where the sense of
rotation is not uniquely definable. This
occurs for the sense of rotation of
| |||||
The formulae of Busing and Levy can be modified using
the equations which follow (BL = Busing and Levy, C =
clockwise, A = anti-clockwise). For any angle
 (
(
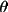 ,
,
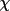 ,
,
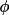 ,
,
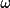 ,
,
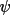 ):
):
 (BL) =
(BL) =
 (C) = -
(C) = -
 (A)
(A)
By introducing the parameters S(
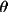 ), S(
), S(
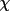 ), S(
), S(
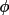 ), S(
), S(
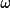 ) and S(
) and S(
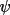 ), the senses of
rotation of the circles of a diffractometer are defined
as:
), the senses of
rotation of the circles of a diffractometer are defined
as:
S = +1 for clockwise rotation S = -1 for anticlockwise rotation
Three equations are produced which convert the angles used on a diffractometer, (DIFF), to equivalent angles in the Busing and Levy system.
 (BL) = S(
(BL) = S(
 ) *
) *
 (DIFF)
(DIFF)
The program will assume the bisecting mode unless the
angle
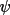 is stored on the bdf
(
is stored on the bdf
(
lrrefl:
, IDN=1011). If, in the
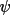 scan mode,
scan mode,
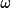 does not fall
within the diffractometer limits (specified in Fields 7-8
on the
diff line) the equivalent
solution is used
does not fall
within the diffractometer limits (specified in Fields 7-8
on the
diff line) the equivalent
solution is used
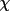 = -
= -
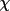 ,
,
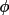 =
=
 +
+
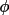 ,
,
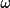 =
=
 +
+
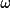
A number of different coordinate systems are used in determining absorption corrections. These are summarized as follows: ( v (system) represents a column vector in a given coordinate system.)
-
The reciprocal lattice system may be non-Cartesian but is not necessarily. In this system a vector v (hkl) is represented as a linear combination of the right-handed reciprocal lattice vectors.
-
The crystal system is a right-handed Cartesian system obtained through the transformation of the hkl system v (crystal) = B v (hkl), where B is the transformation matrix defined using the direct and reciprocal lattice parameters. The B matrix is listed below.
a* b* cos 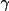 *
*c* cos 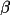 *
*0 b* sin 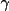 *
*-c* sin 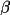 * cos
* cos
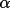
0 0 1/c Calculation of the absorption corrections is done using the coordinates of the crystal system.
-
The
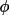 system is a
right-handed Cartesian system which is rigidly
attached to the
system is a
right-handed Cartesian system which is rigidly
attached to the
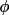 shaft of the
diffractometer. The definition of the axes is
completely arbitrary. For two examples see Busing and
Levy (1967) and Coppens (1970). The ABSORB program
uses the definition of Busing and Levy, i.e., with
all circles set to zero, the x-axis is along the
scattering vector, the y axis is in the direction of
the primary beam, and the z-axis points upward. The
shaft of the
diffractometer. The definition of the axes is
completely arbitrary. For two examples see Busing and
Levy (1967) and Coppens (1970). The ABSORB program
uses the definition of Busing and Levy, i.e., with
all circles set to zero, the x-axis is along the
scattering vector, the y axis is in the direction of
the primary beam, and the z-axis points upward. The
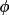 system is
related to the crystal system by the rotation matrix
U as follows:
system is
related to the crystal system by the rotation matrix
U as follows:v (
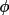 ) =
U v (crystal)
) =
U v (crystal)
Two views of the crystal shape are provided as
options. These are a projection of the crystal shape along
the three cell directions or a stereoscopic view of the
crystal tilted 15° in z and -10° in y. These
options are selected by entering
or
proj
on the
ABSORB line. All plot
information is stored on the plot bdf
stereo
absand the program
PLOTX must be used to
display the selected view on a graphical device.
-
Reads reflection data from the input archive bdf
-
Writes absorption corrections to the output archive bdf
-
Writes crystal shape commands to the plot bdf
abs -
Optionally, writes
HKLlines to the line filepch
remark SEE ALCOCK (1974) AND FLACK AND VINCENT (1980) ABSORB gauss diff c c c c c 0 orient 1 0 0 -30.66 83.32 0 1 0 23.82 34.93 faceml 1 0 0 0.10 faceml 0 1 1 0.15 faceml 0 -2 1 0.05 faceml -3 0 1 0.03 faceml 1 1 -4 0.13 grid 8 8 8 0
ABSORB analyt : Alcock's Analytical Test diff c c c c c 0 orient 1 0 0 -30.66 83.32 010 23.82 34.93 faceml 1 0 0 2.5 faceml -1 0 0 2.5 faceml 0 0 -1 10 faceml 0 1 0 3.75 faceml 0 -1 0 3.75 faceml 0 -1 1 0.883875 faceml 0 1 1 0.883875
-
Alcock N.W. 1970. The Analytical Method for Absorption Correction. Crystallographic Computing. F.R Ahmed, S.R. Hall, and C.P. Huber, eds., Munksgaard. Copenhagen: 271-278.
-
Alcock, N.W. et al. 1972. An Improvement in the Algorithm for Absorption Correction by the Analytical Method. Acta Cyst. A28, 440-444.
-
Alcock, N.W. 1974. Absorption and Extinction Corrections: Calculation Methods and Standard Tests. Acta Cryst. A30, 332-335.
-
Busing, W.R. and Levy, H.A. 1957. High-Speed Computation of the Absorption Correction for Single Crystal Diffraction Measurements. Acta Cryst. 10,180-182.
-
Busing, W.R. and Levy, H.A. 1967. Angle Calculations for 3- and 4- Circle X-ray and Neutron Diffractometers. Acta Cryst. 22, 457-464.
-
Cahen D. and Ibers, J.A. 1972. Absorption Corrections: Procedures for Checking Crystal Shape , Crystal Orientation, and Computer Absorption Programs. J.Appl. Cryst. 5, 298-299.
-
Chidambaram, R. 1980. Absorption Corrections for Single-Crystal X-ray and Neutron Data. Computing in Crystallography. R. Diamond, S. Ramaseshan, and K. Venkatesan, eds., Indian Academy of Sciences. Bangalore, India: 2.01.
-
Coppens, P. 1970. The Evaluation of Absorption and Extinction in Single-Crystal Structure Analysis. Crystallographic Computing. F.R. Ahmed, S.R. Hall, and C.P. Huber, eds., Munksgaard. Copenhagen: 255.
-
Coppens, P. & Hamilton, W.C. 1970. Anisotropic Extinction Corrections in the Zachariasen Approximation. Acta Cryst. A26, 71-83.
-
de Meulenaer, J. and Tompa, H. 1965. The Absorption Correction in Crystal Structure Analysis . Acta Cryst. 19, 1014-1018.
-
Flack, H.D. and Vincent, M.G. 1980. Absorption and Extinction Corrections: Standard Tests. Acta Cryst. A36, 682-686.
-
Gabe, E.J. 1980. Diffractometer Control with Minicomputers. Computing in Crystallography. R. Diamond, S. Ramaseshan, and K. Venkatesan, eds., The Indian Academy of Sciences. Bangalore, India: 1.01.
-
Grochowski, J. Personal communication.
-
Tibballs, J.E. 1982 The Rapid Computation of Mean Path Lengths for Spheres and Cylinders. Acta Cryst. A38, 161-163.
-
Tibballs, J.E. Personal communication.