RFOURR is a reverse Fourier transform program which produces structure factor magnitudes and phases from an input electron density map. The electron density map may be prepared in a number of ways. The fastest, and least useful, is by means of the XTAL program FOURR . In this case the electron density is simply transformed back into the A and B which produced the original map. On the other hand FOURR will often be the source of the electron density map which will be filtered by some means to improve the quality of the map.

RFOURR uses a set of (fast) Winograd Fourier transform subroutines (Silverman, 1977) to carry out the transformation. The subroutines are restricted to certain grid parameters. These are given in Table 1. When the input map is generated these restrictions must be observed.In addition the input map must contain the density of the whole unit cell. For example, if the cell direction is divided into 30 grids then points 0 through to point 29 only must be present in the input map.

Table 1: Grid sizes allowed for in RFOURR

The last restriction is that the summation order of the map must be consistent with the sort order of the reflections on the bdf. The algorithm in RFOURR depends upon the sort order of the reflections and the summation order of the input density map. Table 2 gives the relationship between the two parameters in terms of the instructions used for SORTRF and FOURR .

Table 2: Reflection Order Related to Map Directions

If the sort order is not established by the SORTRF program it may be specified on the RFOURR line. In addition to the sort order another related parameter is required. They are a set of signals which indicate whether the miller indices on the bdf are negative. This information is stored on the bdf by SORTRF or may be explicitly stated on the RFOURR line. The sort 3 option must be used in SORTRF. Note that the slow changing index must have no negative indices. That is for triclinic the hemisphere of data is always +++, -++, +-+, --+ when a lhk or lkh sort has been specified. For monoclinic only +++ and -++ would be present. For orthorhombic only +++ would be present on the file.

The most efficient order for a Fourier transform is over the short axis first (across), medium length axis next (down) and finally the long axis (layer). This produces the fewest groups of reflections and results in the most efficient Fourier transformations.

RFOURR depends upon the input map being of the entire unit cell (no more, no less) with all symmetry equivalent points having identical electron density. The XTAL system stores only the unique asymmetric set of reflections in the bdf. The following algorithm in employed. As each line of the input map is loaded it is transformed, 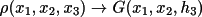. The second sum coefficients G are stored until one layer, all for a given 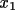, has been treated. The layer is tranformed for all 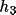values to produce P( , , 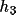) coefficients of the third sum direction. This is the massive array required by the FFT algorithm. The third direction summation is driven by the input bdf, resulting in only the phases of the unique asymmetric set of reflections within the resolution of the input map being calculated. 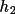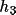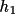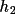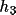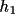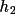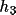In this summation the F( , , ) is produced and stored on the output bdf as A( , , ), B( , , ) and ( , , ).

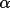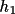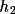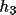The RFOURR calculation produces four structure factor coefficients: the calculated magnitude (CAL); the phase (PHI) and the complex components (A & B). These coefficients are inserted into the lrrefl: packets of the output bdf. In the simplest case these coefficients CAL, A, B and PHI will the standard structure factor items represented by the ID numbers n800, n801, n802 and n700, respectively. In other cases, the ID numbers will be determined by the type of density map, and the nature of the filtering that it has undergone. For the non-standard case the user may define the ID numbers of the output items with the idnums line.

The ID number of the input coefficient (OBS) may also defined on this line. The default is Frel with dispersion removed (n701), or if this is not present, Frel (n304). Note that the input coefficient is only important if the results are to be printed (see the pr option on the RFOURR line) and the calculated R -factor (see below) is to be meaningful.

Map Resolution And Precision

An R factor 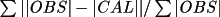is calculated during the transformation. This R factor is useful if the input density has been filtered. For an input map prepared by FOURR the result is of academic interest since it should be zero (OBS->density->OBS results in no differences in OBS). If, however, there is a reduction in resolution by restricting the fineness of the grid during FOURR then the resulting OBS produced by the back transform will be distorted and a higher R value will result.

When RFOURR is applied the resolution of the input density map will determine the extent of the reflections for which phases are determined. In order that every reflection be phased it is necessary that the input map have a resolution of at least 2 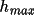, 2 and 2 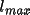grid points respectively in the x,y and z directions. Anything less will result in the high order reflections being left unphased. Output idems for these reflections are set to voidflg:.

To avoid the indeterminacy associated with phasing structure factors where both A and B are very small, the user may define a threshold via the th option on the RFOURR line. The default value is 0.005. Items for reflections below the threshold, are set to voidflg:.Similarly, if a reflection is outside the limits defined by the maxhkl line, or the values from lrdset: of the input bdf, the output items will be set to voidflg:.

RFOURR lhk

This is a standard run. The inclusion of lhk is only required if SORTRF has not been used to sort the reflection data on the bdf. If SORTRF has not been applied the lhk indicates the sort order l slow; k fast is how the data is supplied (the program will fail if the reflection data is not sorted -- you are strongly advised to use SORTRF ). The output coefficients are Fcal, Acal, Bcal and . No reflection data is printed.

RFOURR ds 2 th .5 print 100
idnums 900 950 951 952 953

This is a special run using reflections from dataset 2. The input comparison coefficient has the idnum 2900; the output coefficients CAL, A, B and PHI are stored as 2950, 2951, 2952 and 2953. The first 100 reflections are printed and only reflections with A and B > 0.5 will be phased. The sort order of the reflection data is extracted from lrdset: and checked against the map orientation.