 |
LSQPL
: Least-squares planes & lines
Authors: George Davenport and
Howard Flack
Contact: Howard Flack,
Laboratoire de Cristallographie, University of Geneva,CH-1211
Geneve 4, Switzerland.
LSQPL calculates the least-squares plane or line
through a set of specified atoms and the angles between
sets of least-squares planes and lines.
LSQPL calculates the equations of least-squares lines
and planes. The method of calculation is that of Schomaker,
Waser, Marsh and Bergman (1959) with the exception of the
method used for obtaining the roots of the cubic equation
in Lagrangian multipliers. Schomaker
et al. used an iterative technique,
whereas LSQPL solves for the roots directly by the general
solution equations. LSQPL also calculates the values and
their estimated standard deviations of the distances of
atoms from the least-squares planes or lines, and of the
angles between planes and lines. The least-squares plane or
line equation is output both in fractional and orthogonal
Angstrom coordinates parallel to
a*, b', c (Rollett, 1965). Cell and
symmetry data are taken from the bdf. The bdf also provides
atom coordinates which may be supplemented or updated with
values read from the line input on
site lines. The atoms
used in the calculations may be supplemented by those
related by a centre of symmetry at a position indicated on
the
plane or
line lines. LSQPL also
permits the selection of defining atoms to be used in the
least-squares plane calculations (
define line) and
non-defining atoms to be used only to calculate the
atom-to-plane or -line distances (
nondef line).
The 2.6 version of this program used the algorithm of
Ito (1981). The algorithm of Ito works well for the
calculation of least-squares planes. However (see Flack,
1990), when applied to the calculation of best-lines
through a set of atoms, it either finds the best-plane or
has poor convergence properties. The much older algorithm
of Schomaker
et al. (1959), used in the X- RAY 76
version of LSQPL by Roger Chastain and Wilson de Camp, has
the considerable advantage of applying to both
least-squares lines and planes. Of the original Davenport
LSQPL XTAL program the input/output sections have been
retained and the calculation section rewritten by Flack.
For the calculation of the variance-covariance matrix of
the plane normal/line direction, it should be pointed out
that the formula
 M =
C
M =
C
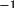 given by Hamilton (1961,1964) [equation 15 of
Hamilton (1961) and equation 22, section 5-8 of Hamilton
(1964)] are incorrect. Hamilton's derivation is based on
taking expectation values of given by Hamilton (1961,1964) [equation 15 of
Hamilton (1961) and equation 22, section 5-8 of Hamilton
(1964)] are incorrect. Hamilton's derivation is based on
taking expectation values of
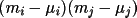 assuming that the three assuming that the three
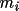 are independent random
variables. In fact
m should be constrained to
be a unit vector, leading to only two independent random
variables, as clearly indicated in the work of Waser, Marsh
and Cordes (1973). The variance- covariance matrix of
m should thus be evaluated
by elimination of one of the are independent random
variables. In fact
m should be constrained to
be a unit vector, leading to only two independent random
variables, as clearly indicated in the work of Waser, Marsh
and Cordes (1973). The variance- covariance matrix of
m should thus be evaluated
by elimination of one of the
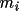 contributing to
C before inversion followed
by augmentation (by propagation of errors), after
inversion, for the eliminated variable. A difficulty in the
calculation of estimated standard deviations of interplanar
or interlinear angles is a sin2 contributing to
C before inversion followed
by augmentation (by propagation of errors), after
inversion, for the eliminated variable. A difficulty in the
calculation of estimated standard deviations of interplanar
or interlinear angles is a sin2
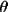 appearing in the
denominator of the expression for converting variance(cos appearing in the
denominator of the expression for converting variance(cos
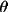 ) into variance( ) into variance(
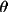 ) [Equation 16 of
Waser, Marsh & Cordes (1973) and equation 26 of Ito
(1981)]. For values of ) [Equation 16 of
Waser, Marsh & Cordes (1973) and equation 26 of Ito
(1981)]. For values of
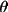 close to 0, this
leads to very large e.s.d.s or division by zero. In LSQPL
the problem is resolved by using a finite difference rather
than a differential formula: close to 0, this
leads to very large e.s.d.s or division by zero. In LSQPL
the problem is resolved by using a finite difference rather
than a differential formula:
![\(\sigma (\theta ) = | arccos[cos\theta \pm \sigma (cos\theta )] - \theta \)](equations/4.33.2-inl-1307.gif) | |
Reads existing atom and symmetry data from the input
archive bdf.
-
Flack, H.D. (1990).
Acta Cryst. In
preparation.
-
Hamilton, W.C. (1961).
Acta Cryst.
14, 185-189.
-
Hamilton, W.C. (1964).
Statistics in Physical
Science.The Ronald Press Company: New
York.
-
Ito, T. (1981).
Acta Cryst.
A37, 621-624.
-
Rollett, J.S. (1965).
Computing Methods in
Crystallography. Pergamon Press: New
York.
-
Schomaker, V., Waser, J., Marsh, R.E. &
Bergman, G. (1959).
Acta Cryst.
12, 600-604.
-
Waser, J., Marsh, R.E. & Cordes, A.W.
(1973).
Acta Cryst.
B29,
2703-2708.
|