A regular grid consists of two sets of equi-spaced lines parallel to two axes. The axes need not be orthogonal, nor do the spacings have to be equal for the two sets of gridlines. The intersection points of these gridlines are the mesh-points, and a regular grid of data therefore consists of functional values at all the mesh points of a finite grid. The smallest parallelogram made by four mesh-points is referred to as a pixel, and the mesh-size in each axial direction is the length of the sides of a pixel parallel to each axis.

Output bdfs produced by FOURR and SLANT contain regular grids of electron density or similar type of data, which are more readily interpreted when suitably contoured. CONTRS allows for the contouring of any layer of such data, or even the contouring of successive layers from the input bdf.

CONTRS is specifically aimed towards production of smooth contours. The various steps in construction of the final plot can be summarized as input of the appropriate layer of data, search for intersections of the contour with all gridlines, chaining of points together to form curves, drawing of the curves with optional smoothing, addition of a title, optional drawing of a border, mesh points and atoms in the vicinity of the plane.

Selection of layers is controlled by the CONTRS input line. The layer numbers correspond precisely with those output by FOURR or SLANT. The absence of any layer specification will cause all layers of the input bdf to be contoured. The resulting contour map will have the same orientation as the printed map unless rotation is requested. A single layer is stored in memory at any one time and the outermost loop in CONTRS is thus over the layers requested.

All contour levels are specified by the LEVELS input line. Three possibilities are allowed for: arith metic (constant interval between levels), geom etric (constant ratio between levels) and direct (input of levels explicitly).

For the arith and geom options, it is necessary to specify a starting level ( start ), a constant increment or ratio between levels ( incr ), and the number of levels to construct from these conditions. For arithmetic intervals, the levels would then be start , start + incr , start +2* incr , ... start +( nc -1)* incr , where nc levels were requested. For the geometric case the levels would be start , start * incr , start * incr **2, etc.

In the case of direct level input, the direct flag on the input line is simply followed by the values of the desired levels. If not all such levels can be accomodated on a single LEVELS input line, then additional LEVELS lines can be input until all levels are entered.

A deficiency of the geom option is that it cannot be used by itself to construct a list of levels which span zero and change sign (e.g. 1.0, 0.5, 0.25, 0.0, -0.25). The negate flag on the LEVELS line will double the number of levels by including all those of opposite sign. In addition the zero level can be explicitly included via the zincl flag. negate and zincl function after all line input has been processed, and hence caution should be exercised when using these options with the arith or direct options.

A maximum of 30 levels is allowed by CONTRS, but it is usually found that when the number of levels exceeds 15 the maps tend to become cluttered.

Each gridline of the layer of data (across and down) is scanned to find all intersections of the contour with gridlines of the layer. These intersections are stored in the order found as coordinates relative to the grid axes.

The current contour value is subtracted from the function value at each mesh-point in turn. Should this result in a numerical zero, a small amount is added to the difference, which has a negligible effect on the resulting map, but insures that no intersections occur at mesh points. Adjacent mesh points exhibiting opposite signs for this difference clearly must bracket an intersection.

The precise location of the intersection may be determined by either linear or cubic interpolation. For the linear case, only two adjacent mesh points are needed, but the cubic requires four neighbouring points which are generally chosen so that the intersection lies between the two central points. For pixels on the edges of the grid this is not possible, and the closest four adjacent points are chosen.

The interpolation over the grid is not a time consuming step in contouring, and cubic interpolation, being only slightly slower and far more accurate, is the program default. Linear interpolation should rarely be necessary, unless as a convenient check that the cubic algorithm is finding all of the points.

Two essential assumptions are made by CONTRS in chaining together successive points to form a curve. The first is that all intersection points lie on the edges of pixels, and never at the mesh-points. This is guaranteed by the minor perturbation of the difference function at the mesh-points described earlier. The second assumption is that only one intersection is found on any edge of a pixel. This is necessarily true with linear interpolation, but is not necessarily the case for cubic interpolation. However, it is extremely unlikely that this will ever happen if adequate mesh-sizes are employed (typically < 0.20 Angstroms), and has never been observed by the author in hundreds of maps.

With these assumptions it is a relatively straightforward matter to search for linkages from one point to another. CONTRS simplifies matters by constructing curves which begin on the edge of the map first. Such open curves must end on an edge also, and searching for them first avoids the creation of curves which are obviously incomplete.

The procedure for chaining is quite simple. The unchained list of points is repeatedly searched from bottom to top until a linkage is found, in which case it is swapped with the point at the bottom of the unchained list and the search is repeated with one fewer point. If no linkage is found, a curve is considered to be complete, and its end point flagged for subsequent curve drawing. Notice here that a contour will comprise several closed and open curves on a typical map.

For linkage purposes no use is made of the previous course of the curve. Rather the obvious requirement, that if a contour enters one edge of a pixel it must exit via one of the other three, is the only criterion used. This means that there are either one, two or three possible links from each point. If several links are found, it is not obvious which is the appropriate one, except that CONTRS avoids the case where curves would cross each other. In such cases CONTRS makes a decision based on which choice leads to the maximum separation between curves inside the pixel, since this avoids the presence of absurdly narrow goose-necked contours. It should be borne in mind, however, that this decision is quite arbitrary and based on aesthetics, where information about the function inside the pixel is missing.

Chaining is the most time consuming part of the contouring procedure and, since it is a sorting process, takes increasingly longer as the number of points per contour increases. Thus for grids with large numbers of mesh points along both axes, and for zero contours on a difference map, several thousand points may have to be searched repeatedly. However in most cases only several hundred points are obtained and the chaining procedure is very fast.

At completion of chaining, the list of unchained points has been transformed into a list of contiguous points on curves, with stored pointers to the end of each curve. The drawing of straight lines between contiguous points on the curves is a trivial exercise, and where a large number of curves are to be drawn or appearance is not important, this is a sensible option.

Drawing smooth curves is also straightforward. CONTRS employs an isotropic four point smoothing algorithm due to Midgley (1979), which makes the direction of the curve at any data point that of a circle through the point and the two adjacent points. This algorithm can be described as a cubic parametric representation in two dimensions of the curve between points 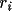and ,

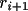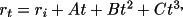
where t ranges from 0 to 1 and the constants A, B and C are determined by the adjacent points on the curve. Separate conditions apply to the terminal points of closed and open curves.

The number of discrete increments in t is governed by the resolution requested on the CONTRS input line. This resolution is closely related to the longest straight line segment used in constructing smooth curves, and is obviously relative to the internal dimensions of the contour map. CONTRS scales all maps to 10 units in the y (down the page) direction, and hence the default resolution of 0.10 is 1 of this dimension. Increasing this value, to 0.20 for example, will reduce the number of plot instructions written to the confile, will hardly be noticed on a high-resolution dot-matrix printer, but any high quality plotting device will display obvious straight line segments.

CONTRS allows for the drawing of both solid lines and dashed lines with regular dash-gap sequences. The assignment of line type to contour level is performed by the lintyp input line, although a default of positive contours solid, zero dashed and negative levels dotted is generally applicable. A distinction is made internally between solid , dashed and dotted lines. Dash and gap lengths are given relative to a y-dimension of 10 units as above, and defaults for these are 0.2 for dash and gap lengths of dashed lines, and 0.08 for dash and gap lengths of dotted lines. Alterations to these characteristics are possible via the dash and dot input lines, which allow for up to 10 different elements in such a sequence, enabling the production of fancy chain-dotted lines if desired.

The border of the contour map can be optionally deleted. The border produced by CONTRS is quite independent of that produced by PLOTX , and in fact the border should be suppressed in PLOTX to avoid any confusion. Mesh-point locations can be optionally plotted as small crosses on top of the final map.

Atoms within a specified neighbourhood of the map will be plotted as large crosses. Atom names of up to four characters can be optionally plotted beneath the crosses. The specification of the neighbourhood is done via the inclusion of the required distance after the atoms flag on the CONTRS control line. The distance is interpreted as being in Angstroms and parallel to the layer axis. Thus the total volume of space within which atoms are generated by CONTRS is the parallelepiped formed by the top and bottom layers plus and minus the specified distance respectively. If no distance is specified a default value of half the distance between layers is used. Off plane atoms are plotted in italics.

The dist includes the off plane atom distances as a second italic text string. A check is made for exact overlap of two atoms at equal and opposite distances which are printed as a single atom label with the distance string "+/-xx.xxx". CONTRS flags the out-of-plane atom labels for printing in italics by preceding the label text string with the vertical bar "|".

There are four sections of printed output produced by CONTRS. The first two sections echo control and contour levels input.

The third section lists contour levels found for each layer, and tabulates along with the contour level the line type, the total number of points found for the level, the number of points purged and the number of individual curves comprising the contour. The number of points purged should always be zero except in very special cases (e.g., a single isolated point at the centre of a peak or hollow), or perhaps where the chaining algorithm is failing. This column is an excellent diagnostic and the presence of any non-zero entries should be carefully investigated.

The fourth section summarizes atoms found within the specified vicinity of the contour map, layer by layer, giving the full name, the number of the symmetry operation which generated the particular atom, the distances in Angstroms (parallel to the border axes) from the top left corner of the map to the atom projected onto the plane, and the distance in Angstroms (parallel to the layer axis) of the atom from the layer.

On conventional monochrome graphics devices (e.g., dot matrix printer or vector pen plotters)CONTRS will produce the map and additional output appropriately scaled to the device by PLOTX . Two lines of title are added below the contour map. The first line gives the compound ID, the lengths of the x-axis and y-axis (across and down the map) in Angstroms, the angle between axes at the lower left of the map and the layer number(s). The second line reproduces the title submitted via the title control line if one was included in the input stream.

CONTRS is currently capable of producing colour graphics output, provided the appropriate device dependent software is incorporated in PLOTX . CONTRS supports six separate colours, and these are assigned to the six groups of output: negative contours, zero contours, positive contours, the border and mesh points, the crosses for atomic sites, the titles and atom names. This colour coding is completely transparent to the user and will not affect output on monochrome devices. Assignment of specific colours to each colour group is performed via PLOTX.

CONTRS flay 16 llay 16 atoms 2.0
LEVELS arith nc 7 st -0.3 in 0.1

In this example, layer 16 of the Fourier map is to be contoured. The levels requested are -0.3, -0.2, -0.1, 0.0, 0.1, 0.2, 0.3, appropriate to a difference Fourier map. All atoms within 2.0 Angstroms of the map will be plotted.

CONTRS slant nn
LEVELS direct -0.3 -0.2 -0.1 negate zincl
LINTYP do 1 3 da 4 4 so 5 7
dash 4 0.2 0.2 0.1 0.1

In this example, SLANT input is specified. The LEVELS line will produce identical levels to the previous example. The lintyp line specifies explicitly what the default assignment of the line types would be. The dash line alters the default dashed line to a chain-dotted line (long dash, short dash, long dash, etc.). Since, in general, SLANT writes only a single layer of data in the slafile, CONTRS will produce only a single map. Atom sites, but not names, will also be plotted.

CONTRS linear nsmooth
LEVELS arith nc 10 start 0.0 incr 1.0

In this case all layers are to be contoured sequentially, with linear interpolation and no smoothing. The levels requested are appropriate to a Fourier of the total electron density.