RMAP is used to calculate maps analogous to electron density maps where each point in the map is a function of 1/R, where R is the conventional R factor ( 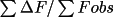). The use of 1/R forces the coordinate of best agreement to be on a maximum. In addition to 1/R maps it is possible to calculate correlation maps (referred to as C maps), or a linear function of 1/R and the correlation. The correlation C function is

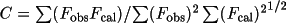at each grid point.

The advantage of C is the fact that it is independent of the Frel scale factor. It is not as "sharp" a function as 1/R, however. It also requires more storage for the additional sums. The maps will show a maximum at the optimum translational position of a fragment in the unit cell. A grid, just like the grid in a regular Fourier transform, is set up in a specified region of the unit cell and structure factors are calculated for a selected subset of reflections at each of the grid points. The values of the calculated structure factors are used to calculate R or C or a linear combination of R and C, at each grid point. A linear combination which gives numbers on a convenient scale has been defined as:

D = {10(1-W)C+1}{(W/R)+1}

The values of D are written to a MAPfile in the same format as that produced by FOURR . MAPmay be used with PEKPIK to search for the maxima. The highest maximum is reported in the RMAP output. The factor W is a factorial weight. If W=1, only R contributes to D, while if W=0, only the correlation coefficient contributes to D. When W=1 is used, 1/3 the amount of storage is required.

It is not usually necessary, or desirable, to include all reflections in the search procedure. Much time can be saved if only the strong reflections, at an appropriate level of resolution, are used in the promotion of D values. It may be necessary to include a small number of weak reflections to control the scale factor. Perhaps a better method for this is to use GENEV with all data to establish a physically realistic Frel scale factor before using RMAP. It is useful to start with low resolution data and a coarse grid. The program is set to use 0.3 Angstrom steps over the whole unit cell with all reflections included in the calculation as default parameters.

Initially when no positional information is available the number of atoms in the fixed fragment will be zero and the calculation will be made only on the translated fragment. After a fragment has been positioned, the first fragment may be declared as fixed and any additional fragment atoms can be designated as translated. This feature allows molecules to "grow" and allows use of the program where there is more than one molecule in the asymmetric portion of the unit cell.

In the initial pass over the bdf data the contributions of all the atoms to the structure factor components A and B, as a function of the symmetry operations, are saved as separate quantities. The selected reflections are written to a scratch file. On the second pass the structure factors are calculated as a function of all the grid points. This is accomplished by using the sums of A and B at each symmetry point and the trigonometric identities:

cos( x + y ) = cos x cos y - sin x sin y

sin( x + y ) = cos x sin y + sin x cos y

From these identities each step y can be applied to each geometrical A and B part of the structure factor ( cosx, sinx ) and the complete structure factor at the step formed by summing only over the number of symmetry operations and not over the number of atoms in the fragment.

The input bdf must have 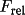or 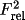, and a set of atomic coordinates with an overall or with individual isotropic thermal displacement parameters. The atoms must be loaded (with ADDATM ) as one or two subsets. The first subset, which may be null, contains the atoms of a fragment which is to remain fixed during the search. The second subset (which must not be null) consists of the atoms to be translated during the search. Atom sites are listed by entering reset psta 4

RMAP iso map weight 0.1       
bounds 0 .125 .0078 0 .125 .0078 0 .125 .0078       
PEKPIK       
plimit *3 12 80

A compound with cell dimensions a=20.515, b=21.31, c=17.128 is searched over 1/512 of the unit cell near the origin, in steps of 1/128 of each cell edge. The resulting RMAP is then searched for maxima. The D function calculated is weighted by 0.1 in terms of 1/R and by 0.9 in terms of C.