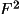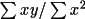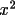A DIFDAT calculation reads an existing Archivecontaining cell and symmetry information, and reads intensity data from a diffractometer generated file, or from line images. The diffraction data may be input as raw intensities, net intensities, or F data.

The nature of the input data is specified in the DIFDAT line (as cad , dat , etc.). DIFDAT processes this data, and converts it into the quantities needed in the scaling process. The processed data is output as an archive bdf suitable for input to SORTRF (for sorting and averaging) or ADDREF (for data reduction). Note that DIFDAT requires that there is an input archive bdf which has been previously created by STARTX , etc. Note also that it is possible to process the diffractometer data in a non-conventional setting and subsequently transform data to a conventional set of axes (see Example 4). The following methods may be used to enter data.

dat mode ( datalines)

Enter the diffraction data from data lines in the input stream. The contents of data lines are specified with a fetch line. See later section on data lines and the third example.

bdf mode

The diffractometer data is read from the archive bdf. It is possible to add this data to the archive bdf with CIFIO.

sie mode (file .sie)

Enter Siemens diffractometer data from a text file .sie. This file is either generated directly by the diffractometer software or is a binary file which has been converted to an ascii text file. The program siecon.f is available from the Xtal FTP site ( see Preface) for this purpose.

cad mode (file . cad)

Enter Enraf-Nonius CAD4 diffractometer data from a text file .cad.

niv or nidmodes (file . nic)

Enter the older Nicolet/Syntex/Siemens diffractometer binary data formats from a file .nic. Specifying the Siemens/Nicolet/Syntex file is complicated because it has a binary format and is therefore dependent on the controlling processor. For a Nicolet controlled by a Data General computer, the code nid is entered on the DIFDAT line. For a Siemens controlled by a VAX computer, the code niv is used. For a Nicolet connected to any other machine, changes will need to be made to the routine DD32. This option also outputs the intensity data as data lines on pch(for any subsequent modification of input data) .

tsu mode (file . tsu)

Enter the standard data file collected at the Tsukuba Photon Factory on the file . tsu.

rd5 mode (file . rd5)

Enter AFC5 and AFC6 Rigaku diffractometer files on the file . rd5.

When raw data is entered the nett intensity is calculated according to the following scheme:

Attenuator	= value selected from the attenuator table
Timescale	= (ScanTime/2) / BackgroundTime
Background	= TimeScale*(Background1 + Background2)
Relative Intensity	= ScanCounts*Attenuator - Background
I	= Attenuator*( ScanCounts + TimeScale*Background)
	= TotalCounts

If raw diffractometer data is read, the decoded quantities are first placed on the intermediate bdf. This file is then searched to separate the 'normal' measurements from the 'standard' measurements. Normal refers to a measurement made in the course of scanning all reflections, and standard to a group of reference reflections for which measurement is made at regular intervals.

No more than 10 different reflections may be designated as standards. There may be as many measurements of the groups of standards as can be held in memory using four words per stored reflection per group measurement. The method of identifying normal and standard reflections will vary according to the diffractometer, and the method of processing data discussed above. If the reflection is coded as a standard, the I, the total counts, a signal, and the sequence number of the measurement are stored. This operation requires that the reflections designated as standards appear sequentially and in groups with the same number of standards at each encounter. The sequence numbers of the standards are stored for use in forming the scale factors which will be used to compensate all reflections for any drift in the standards over the data gathering process. In the case where no sequence numbers are available from the diffractometer, they will be generated from the count of the reflection input lines.

Two methods are available to specify which reflections are to be used as standards. The first is to specify the coded information in the input which may be used to identify a standard reflection. The second is to give an ordered list of h, k, and l values for the reflections to be treated as standards.

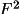If the input data has been partially preprocessed so that I, , or F is not known, the user may specify an average error to be applied to I, 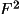, or F to give an estimate of the I for further calculation. During the course of the data translation and intensity calculations, the standards measurements are stored in memory. These standards are used for two purposes; first is the establishment of a set of scale factors based on the counts of all the standards, second is the preparation of an instability factor. This factor is based on the spread and trend of the measurement of the standard reflections and used in the estimation of sigmas.

Application of Instability Factors

The form of the instability factor is specified as the inst option on the DIFDAT line. This option determines how the instability factor is used to modify the I based on counting statistics for the single observation of a reflection. No attempt will be made to calculate the values of slopes or intercepts if the standards have been measured less than seven times during the data gathering procedure.

For all the instability factor options, the average value of the total counts for each measured standard reflection is calculated as follows.

	∑ (total counts of jth standard)
Average total count of jth standard =	-----------------------------
	no. of observations of jth standard

From this average value and the individual measurements of each standard the external variance may be calculated for each standard. This gives an independent measure of the variance over and above the variance based on counting statistics.

external variance =	-------------------------

where TC is the total counts of the jth standard, ATC is the average total counts of the jth standard and NTO is the number of times the jth standard was observed.

Instability options ( inston the DIFDATline)

Option	Meaning
0	Only the counting statistics are used in calculating (I), the square root of the total counts taken for a given observation.Default if no inst option is specified.
1	Only the slope of a line through the origin is calculated.
	The customary least squares fit of a set of data to a line of the form of y =mx + b is carried out. In this analysis the variable x is the square of theaverage total counts for each standard reflection and the variable y is thedifference between the external variance and the average total counts. The sumis over the different standard reflections. m =
2	Both the slope and intercept of the line are determined.
	The valuesof x and y are the same as in option 1 and the sums are over the N standards. slope = N* [∑x ∑(y/N) - ∑xy ] / [(∑x) - ∑ ] intercept = [∑y - slope * ∑x] / N
3	The slope, determined in option 2, is used and the interceptvalue is left as zero.
4	Same as option 3 except that the user supplies the values
	of the slope and intercept in the DIFDAT line behind option inst m is the second field beyond inst . b is the third field beyond inst .

During reflection processing estimated I values are compared with the estimated I, based on intensity counting statistics. When I > n* I a reflection is considered to be "observed" and is assigned an rcode=1. If I < n* I a reflection is considered to be a "less than" and is assigned an rcode=2. The value of n may be specified in the DIFDAT line by the use of the obst n specification. The value of n=2 is the default. If n=0 is specified, all reflections will be given rcode=1 values.

If the option obth is specified, the n I value will be stored for the value of I. This option is a controversial one in that it imposes a feature reminiscent of the threshold of observability characteristic of photographic intensity measurements. The default, nobth , causes the calculated values of I to be stored in the output file. This means that negative as well as positive values are stored for reflections with weak intensities.

DIFDAT was originally designed on the assumption that the diffractometer output will be similar to that produced by a Picker FACS (see the Examples). As such diffractometer lines are assumed to start with the line identifier data. If this is not the case it will be necessary to preset the input line identifiers by entering setid data and follow the last data line with a blank setid ( see System). The fetch line is used to specify the order and the type of data entered on the data line. Fields on the data lines must be separated by blanks. If they are not, it will be necessary to read these lines in fixed format mode using the field line (see CONTROLS section).

The alternative method of entering the diffractometer data involves the implementation of local routine (e.g. DD32) to read the data lines. The first two examples show the input used in this approach; the last two when data lines are entered.

The option nap on the DIFDAT line, and the two input lines setscl and genscl, control the application of scale factors to the intensity data. The nap option suppresses the application of any scale factors to the intensities.

The setscl line specifies a scale factor which will will supercede that for a group of standards. The genscl line signals that the scales will be generated from the standard reflection groups and smoothed over a specified number of scale groups. If a genscl line is not entered, a scale factor must be entered for each standard group using setscl lines. If a GENSCLline is entered, the setscl lines will be used to override one or more of the generated scale factors.

genscl controls the smoothing of scale factors over a specified number of standard groups. Statistical fluctuations can occur due to natural counting errors or too few standards being observed. The default smoothing range is five groups forward and five groups backward.

It is possible that the scale discontinuities are not statistical. This occurs if there is a change in the radiation source or a degradation of crystal. In this case, discon lines may be used to point to the standard groups at which the scale discontinuities are real. The smoothing function will not span these groups. Note that the serial numbers of the last member of a group of standards are used in the setscl and discon input lines.

DIFDAT assumes that data starts with a group of standards and ends with a group of standards. This arrangement is not mandatory but warning messages are written if this condition is not met and a careful assessment of the scale factors should be made.

DIFDAT is a two pass program. The data is first processed for the estimation of scale and instability factors. It is then reread and the scaled intensities are written to the output archive bdf. The data written into logical record lrrefl: are the packed hkl (IDN=1), the net intensity (IDN=1300), I (IDN=1301), and rcode (IDN=1308).

Printed output of reflection data is specified on the DIFDAT line with the options ( print and raw ). In the first pass the raw intensity data is printed and in the second the scaled reflection data is printed. There is provision for a sample of reflection data to be printed during each pass. Each reflection line is screened for unequal backgrounds and this condition is noted in the optional printed output.

Process a 61 byte-record CAD4 diffractometer file cad.

DIFDAT cad pri 50 excl inst 1 obst 3
attenu 19.14
genscl 2

Process a standard Siemens diffractometer text file sie.

DIFDAT sie pri 50 excl inst 1 obst 2
genscl 3

Process data on data lines

DIFDAT pri 50 eul inst 1 obst 2.0
stands 1 1 2 2
fetch rfn h k l tth omg phi chi irl sir sig
data 1 0 0 2 13.56 6.78 95.68 112.63 6574 135
.............................data lines omitted for brevity
data 1354 12 7 -9 87.42 43.71 15.93 74.14 761 48
genscl 3

Process data for non-conventional setting - full calculation sequence.

title IO11 in non-conventional setting Pnca of Pbcn
STARTX
CELL 10.664 15.838 26.086
sgname -p 2a 2n       :pnca
CELCON c 10
DIFDAT cad excl inst 1
atten 16.8
genscl 2
SORTRF hkl merge 1 cut
COPYBDF a tem         :store merged refln data on tem
title IO11 in conventional setting Pbcn
STARTX
CELL 15.838 26.086 10.664
cellsd .004 .006 .002
sgname -p 2n 2ab      :pbcn
CELCON c 120
CELCON o 40
CELCON h 200
ADDREF
reduce itof rlp3
transf 0 1 0 0 0 1 1 0 0
bdfin file tem hkl irel sigi rcod

This is an important example because it shows a full Xtal run from STARTX to ADDREF involving the DIFDAT calculation. It also demonstrates how to process diffractometer data collected with non-conventional axial settings, and to subsequently transform it the conventional space group setting. The components of this run are: generate an archive bdf for the non-convertional space group; process the CAD4 data in this space group; sort and merge the intensity data in this space group; save the current archive bdf containing the merged data on file tem ; create a new archive bdf with the conventional space group settings; reduce the reflection data by inputting the intensity data from the file tem (see the bdfin line) and transform the indices to match the conventional axes. The output archive file contains an unique set of Frel values for the space group Pbcn.