 |
BONDAT
: Generate atom coordinates
Authors: Ruth Doherty, Jim
Stewart and Howard Flack
Contact: Howard Flack,
Laboratoire de Cristallographie, University of Geneva, 24
quai Ernest Ansermet, CH-1211 Geneve 4, Switzerland
BONDAT generates the coordinates of atoms whose
positions can be inferred from the geometry of previously
placed atoms.
BONDAT generates inferred atomic coordinates from
known atomic coordinates. All the known atomic coordinates
of a structure are loaded into memory. Once loaded, a
series of input lines denoted by
CALCAT are supplied.
There are nine types of
CALCAT input lines
described in detail below.
Each line generates a different configuration of
inferred atomic coordinates from known coordinates. The
generation is carried out based upon matches of the
character strings which are the atom identities. One
feature of the program is that, once generated, new atoms
become part of the list of atoms in memory and can
therefore be used in further generations. Caution should be
exercised when using this feature to extend chains because
of the danger of the magnification of errors in the
placement of the "known" atoms.
All the atoms which are used for generation must have
coordinates which are geometrically correct for the
generation to be carried out. The generating atoms must be
located so that they form a connected set. There are no
tests made in the BONDAT program to assure that this
restriction is met. The use of BONDLA following BONDAT will
serve as a check on the correctness of the locations of the
generating atom coordinates.
In archive update mode, BONDAT adds the
CALCAT generation
instructions as well as the new atom sites to the archive.
This information can be used by the least squares routine
CRILSQ
to implement
riding atom model refinement.
The geometric arrangements of the nine types of
calculations permitted are:
Given atoms P1 and P2, atom P3 will be generated at
a distance D from P2, with a bond angle P1-P2-P3 of
0.0°. Note that P3 lies in the same direction from
P2 as does P1. This calculation type is useful in the
generation of hydrogen-bonded hydrogen atoms.
Given atoms P1, P2, and P3, atoms P4 and P5 will be
generated at a distance D from P2 with a bond angle
P4-P2-P5 of 109.5°. The plane P1-P2-P3 will be
perpendicular to the plane P4-P2-P5. If the bond angle
P1-P2-P3 is about 109°, the resultant geometry
about P2 will be tetrahedral. This type of calculation
can be used to produce the hydrogen atoms of a methylene
group (-CH2-) in a tetrahedral chain.
Given three atoms P1, P2, and P3 with bond angle
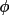 , three atoms
will be generated, all at a distance D from P3.
Initially, P6 will lie in the plane of P1-P2-P3 with a
bond angle P2-P3-P6 of 109.47° and a dihedral angle
P1-P2-P3-P6 of 180° (an anti-periplanar
arrangement). From this initial arrangement it is
possible to rotate P6 counter-clockwise by , three atoms
will be generated, all at a distance D from P3.
Initially, P6 will lie in the plane of P1-P2-P3 with a
bond angle P2-P3-P6 of 109.47° and a dihedral angle
P1-P2-P3-P6 of 180° (an anti-periplanar
arrangement). From this initial arrangement it is
possible to rotate P6 counter-clockwise by
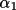 ° about the P3-P2
bond. ° about the P3-P2
bond.
P4 and P5 will form an angle of
109.5° about P3, and the plane P4-P3-P5 will be
perpendicular to the plane P2-P3-P6. This calculation
type may be used to generate the hydrogen atoms on a
methyl group at the end of a tetrahedral chain
(tetrahedral terminal).
Given four atoms P1, P2, P3 and P4 such that P1 is
attached to P2, P3 and P4, atom P5 will be generated at a
distance D from P1 to complete an approximately
tetrahedral arrangement of four atoms about P1 with the
three angles P5-P1-P2, P5-P1-P3 and P5-P1-P4 all equal.
median
is a better choice than
methyn
for cases where the angles subtended at P1
by P2, P3 and P4 are far from the tetrahedral
angle.
Given three atoms P1, P2, and P3, atoms P4, P5, P6,
and P7 will be generated such that P4 and P5 bear the
same relationship to the input atoms as in the
sqrpln
case. P6 and P7 will each be at a distance
D from P2. The straight line P6-P2-P7 will be
perpendicular to the plane of the other atoms. If the
angle P1-P2-P3 is about 90°, the resultant geometry
about P2 will be octahedral.
Given three atoms P1, P2, and P3, atoms P4, P5, and
P6 will be generated such that all six atoms lie in a
plane and form a six membered ring. The distances P1-P6
and P3-P4 will be D, and the distance P2-P5 will be 2*D.
If the angle P1-P2-P3 is
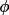 , then the angles
P2-P1-P6 and P2-P3-P4 be 180-( , then the angles
P2-P1-P6 and P2-P3-P4 be 180-(
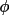 /2). If the
distances P1-P2 and P2-P3 are approximately equal and the
angle P1-P2-P3 is about 120°, the geometry of the
six atoms will be hexagonal. /2). If the
distances P1-P2 and P2-P3 are approximately equal and the
angle P1-P2-P3 is about 120°, the geometry of the
six atoms will be hexagonal.
Given three atoms P1, P2, and P3, atom P4 will be
generated at a distance D from P2. To understand the
position of P4 relative to the generating atoms, consider
a new Cartesian coordinate system (x',y',z') in which the
x'y' plane coincides with the plane of the three
generating atoms. The +z' direction is defined by the
cross product (P1-P2)x(P3-P2). The +y' direction is
defined by the vector P3-P2, and +x' lies in the
direction which gives a right-handed system with y' and
z'. The projection of the vector P4-P2 onto the x'y'
plane forms an angle
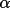 1 with the
vector P3-P2. The cross product (P3-P2)x(P4-P2) lies in
the +z direction. The angle 1 with the
vector P3-P2. The cross product (P3-P2)x(P4-P2) lies in
the +z direction. The angle
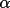 2 is the angle
between the vector P4-P2 and the x'y' plane. If 2 is the angle
between the vector P4-P2 and the x'y' plane. If
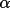 2 is between 0
and 180°, P4 will lie above the x'y' plane (i.e.,
in the +z direction); if 2 is between 0
and 180°, P4 will lie above the x'y' plane (i.e.,
in the +z direction); if
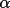 2 is between
180° and 360° (or 0° and -180°),
P4 will lie below the x'y' plane. As an example, consider
a chain of three carbon with two hydrogen atoms attached
to C2 (viz., H21 and H22) are to be generated using 2 is between
180° and 360° (or 0° and -180°),
P4 will lie below the x'y' plane. As an example, consider
a chain of three carbon with two hydrogen atoms attached
to C2 (viz., H21 and H22) are to be generated using
genral
calculations, two
CALCAT lines are
needed, one for each hydrogen. The plane defined by C2,
H21 and H22 must bisect the C1-C2-C3 angle, so for both
H21 and H22 the angle
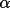 1 is
125.25° (i.e.,(360-109.5)/2). The bond angle
H21-C2-H22 will be 109.5° (so that the arrangement
around C2 will be tetrahedral) and the plane defined by
C1, C2 and C3 will bisect that angle. Therefore, 1 is
125.25° (i.e.,(360-109.5)/2). The bond angle
H21-C2-H22 will be 109.5° (so that the arrangement
around C2 will be tetrahedral) and the plane defined by
C1, C2 and C3 will bisect that angle. Therefore,
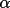 2 will be +54.75
for one of the hydrogen atoms and -54.75 for the other.
Although the generation of hydrogen atoms in a
tetrahedral chain can be accomplished more easily with a 2 will be +54.75
for one of the hydrogen atoms and -54.75 for the other.
Although the generation of hydrogen atoms in a
tetrahedral chain can be accomplished more easily with a
tetchn
calculation, the results will be the same
if the two
genral
calculations described here are used
instead.
Given four atoms P1, P2, P3, and P4 such that P1 is
attached to P2, P3 and P4 with bond angles about P1 all
about 109°, atom P5 will be generated at a distance
D from P1 to complete the tetrahedral arrangement of four
atoms about P1. This calculation type can be used to
generate methynyl hydrogen atoms.
The cell parameters and atomic coordinates must be
supplied from the bdf. Generated atoms are added to the end
of the atom list in memory if they were not already present
in the bdf and may be specified as input for any subsequent
CALCAT request. If a
generated atom was read in from the bdf, the coordinates
read in from the bdf are superseded by the newly generated
coordinates.
A summary is written after all the
CALCAT lines have been
handled. Listed in the summary, for each generated atom,
are the atom name, the generated coordinates, the atom type
pointer (referring to
lrscat:
in the bdf), the name of the atoms used in the
generation and the bond distance.
Caution:
it is important to remember that no check is
made to determine whether the set of atoms used in the
generation of any new atom(s) is a connected set. If the
coordinates in the file for the set of atoms used in some
generation are not the coordinates of a connected set, but
rather the symmetrically equivalent coordinates of points
that are not connected, the coordinates of the generated
atom may not be the desired ones.
-
Optionally reads input archive bdf
-
Optionally writes output archive bdf
-
Optionally writes atom lines to file
pch
-
In update mode, spawns reentrant ADDATM input
file
.ad1
The coordinates of all of the hydrogen atoms attached
to the ring in salicylic acid may be generated by BONDAT.
The input shown above will cause BONDAT to read the
coordinates of all of the atoms in the bdf and use them in
the calculations. The hydrogen atoms will be located at a
distance of 1.0 Angstrom from the carbon atoms to which
they are attached and will have the same atom numbers as
the carbon atoms to which they are attached (e.g.
H3is attached
to
C3).
|