|
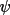

|
0° | 45° | 90° | 135° | 180° |
P(ψ
 | 3.) | 3.) |
.65 | .27 | .03 | .004 | .002 |
P(ψ
 | 1.) | 1.) |
.34 | .25 | .13 | .06 | .05 |
Direct methods procedures depend critically
on being able to predict the value of
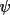
 and on being able to apply triplet relationships
as a series of equations. For large values of A,
and on being able to apply triplet relationships
as a series of equations. For large values of A,
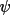
 has a high probability of being 0. and this makes
large-A triplets particularly important for these
processes.
has a high probability of being 0. and this makes
large-A triplets particularly important for these
processes.
For the quartet structure invariant relationship
the value of
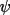
 depends principally on the probability factor
depends principally on the probability factor
For uniform-atom structures
b tends to 1/N. The
probability distribution of
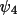 , ignoring the
cross-vectors magnitudes E(
, ignoring the
cross-vectors magnitudes E(
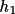 +
+
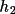 ), E(
), E(
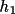 +
+
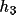 ), and E(
), and E(
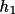 +
+
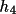 ) (referred to later as
) (referred to later as
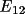 ,
,
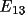 ,
,
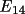 ), may be written as
follows (Hauptman, 1976)
), may be written as
follows (Hauptman, 1976)
This function is similar to P(
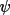
 |A), except that the value of B will tend to be
much smaller for large structures. The probability
distribution of
|A), except that the value of B will tend to be
much smaller for large structures. The probability
distribution of
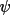
 is dependent on more than the principal vectors
that go to make up B and is more correctly
is dependent on more than the principal vectors
that go to make up B and is more correctly
where Z is a function of the seven vectors E(
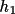 ) to
) to
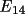 . An important property
of the probability expression (4.24) is that if the
cross-vectors are large, then expression (4.23) holds, but if
the cross-vectors are
small then expression (4.24) approximates as
. An important property
of the probability expression (4.24) is that if the
cross-vectors are large, then expression (4.23) holds, but if
the cross-vectors are
small then expression (4.24) approximates as
The importance of this result may be illustrated for a fixed value of B (for example, 3.) and for small and large cross-vectors (XV)
ψ
 |
0° | 45° | 90° | 135° | 180° |
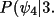 ,
large XV) ,
large XV) |
.65 | .27 | .03 | .004 | .002 |
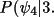 ,
small XV) ,
small XV) |
.0001 | .0003 | .002 | .005 | .007 |
Because of the dependence of
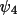 on the magnitude of the
cross-vectors, quartets are usually grouped into two
classes according to the sum of cross-vector
magnitudes.
on the magnitude of the
cross-vectors, quartets are usually grouped into two
classes according to the sum of cross-vector
magnitudes.
If XVsum is greater than a certain threshold (e.g.
XSHI), a quartet is referred to as a
positive quartet (because
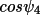 should be positive). If it
is less than a lower threshold (e.g. XSLO), a quartet is
known as a
negative quartet (because
should be positive). If it
is less than a lower threshold (e.g. XSLO), a quartet is
known as a
negative quartet (because
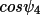 should be negative).
GENSIN estimates the value of XVSUM and various procedures
can be adopted by the user to control the generation of
quartets using this sum.
should be negative).
GENSIN estimates the value of XVSUM and various procedures
can be adopted by the user to control the generation of
quartets using this sum.
The normalization program,
GENEV
, converts known structural information into one or
more group structure factors G(h) for each reflection.
These group structure factors are used in
GENEV
to calculate an expectation value for
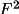 (h) where M depends on
the number of molecular fragments and the nature of the
fragment information (see
(h) where M depends on
the number of molecular fragments and the nature of the
fragment information (see
GENEV
for details).
GENEV
outputs the group structure factor values as the
magnitude G(h) and the phase g(h). Knowledge of the
structure influences the values expected for
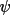 . If the atomic
parameters are known to a certain precision, then G(h) and
g(h) values (which in this instance are the same as F(h)
and
. If the atomic
parameters are known to a certain precision, then G(h) and
g(h) values (which in this instance are the same as F(h)
and
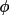 (h)) may be used to
predict
(h)) may be used to
predict
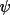 to the same
precision. The group structure factor is in fact an
important component in the conditional probability
expressions for
to the same
precision. The group structure factor is in fact an
important component in the conditional probability
expressions for
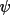
 and
and
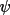
 .
.
Main (1976) modifies the value of A to the form:
where
The correspondence between
a' and
a in expression (4.20) is
quite apparent when the only knowledge of a structure is
its atomic content. Then each <
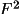 (h)>=
(h)>=
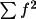 (s); each
(s); each
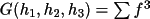 (s) and
a' =
a. With increasing
structural information the value of
a' may differ
substantially from
a. The most important
term in expression (4.29) is the joint group structure
factor G(
(s) and
a' =
a. With increasing
structural information the value of
a' may differ
substantially from
a. The most important
term in expression (4.29) is the joint group structure
factor G(
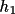 ,
,
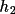 ,
,
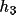 ) which is calculated
directly for each invariant from the known structural
information (see Main, 1976). This calculation is,
however, a time-consuming task even for small structures.
A more efficient approach involving a minimal loss in
precision is the use of the individual group structure
factors of the form (Hall, 1978):
) which is calculated
directly for each invariant from the known structural
information (see Main, 1976). This calculation is,
however, a time-consuming task even for small structures.
A more efficient approach involving a minimal loss in
precision is the use of the individual group structure
factors of the form (Hall, 1978):
This approximation applied to quartet relationships gives
where
In this way fragment information is used to predict
the distribution of
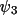 and
and
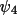 according to
according to
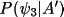 and
and
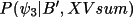 . Most
importantly, however, the probability terms A' and B'
from (4.30) and (4.31) are complex
. Most
importantly, however, the probability terms A' and B'
from (4.30) and (4.31) are complex
with the phase values
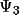 and
and
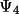 , which are estimates of
, which are estimates of
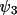 and
and
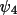 , respectively. The
reliability of
, respectively. The
reliability of
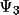 and
and
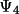 as phase estimates
depends on the precision of the structural information,
and the magnitude of A' and B', respectively. For
random-atom structures (i.e., fragment information type-1
in
as phase estimates
depends on the precision of the structural information,
and the magnitude of A' and B', respectively. For
random-atom structures (i.e., fragment information type-1
in
GENEV
) A' = A and B' = B, and
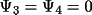 .
If random-fragment (type-2) information is used in
.
If random-fragment (type-2) information is used in
GENEV
, the
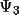 and
and
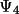 values are also assumed
to be zero (this is a limitation of using approximation
(4.32) instead of (4.31)).
For type-3 and type-4 fragments information the values of
values are also assumed
to be zero (this is a limitation of using approximation
(4.32) instead of (4.31)).
For type-3 and type-4 fragments information the values of
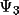 and
and
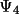 may be non-zero. In the
following description and input line formats
may be non-zero. In the
following description and input line formats
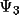 and
and
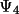 values are referred to
as the fragment
values are referred to
as the fragment
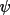 estimates
"QPSI".
estimates
"QPSI".
In addition to generating structure invariants,
GENSIN provides the conditions for the origin and
enantiomorph definition of the cell. Fixing the origin and
enantiomorph is a necessary first step in the
GENTAN
phase extension process. It is performed
automatically; the user may, however, override this
procedure using phases selected according to the
definitions output by GENSIN. The conditions for specifying
the origin in terms of structure factor seminvariant phases
is detailed by Hauptman and Karle (1956) and Karle and
Hauptman (1956). Application procedures for applying these
conditions are described by Stewart and Hall (1971), Luger
(1980), and Hall (1983).
It should be noted that for GENSIN and
GENTAN
the seminvariant vector conditions are always in
terms of the input indices. It is therefore unnecessary to
transform centred indices to primitive indices for the
purposes of origin specification. Details of the
seminvariants vectors for centred space groups are
described by Hall (1982).
The origin of a cell is fixed by specifying the structure factor phases of p linearly-independent reflections. The value of p ranges from 0 to 3, and is determined by the space group symmetry.
Any reciprocal lattice vector h is a linear combination of p origin defining vectors h(1). . . h(p)
where
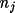 is any integer value. This
relationship may be expressed as the vector
transformation
is any integer value. This
relationship may be expressed as the vector
transformation
where n is the set of integers n(1), . . .n(p) and H is the set or origin defining reflections h(1), . . . h(p). The linear relationship of a reflection h to the set of origin defining reflections H is given by
A reflection vector h may also be transformed into the seminvariant indices u by the operations
and
where V is the seminvariant vector matrix and m the seminvariant moduli (Hauptman and Karle, 1956). A necessary requirement of any set of origin defining reflections is that the matrix of seminvariant indices U
has the magnitude
The linear relationship of any structure factor phase
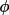 (h) may be
expressed in terms of the
u from (4.37) as:
(h) may be
expressed in terms of the
u from (4.37) as:
If Q is defined as the set of origin defining phases
The seminvariant phase due to linear relationship of h to H may be derived from the linear combination of these phases (Hauptman and Karle, 1956)
If seminvariant phase q(
h ) is equal, modulus
 , to the phase of
vector
h, then the value of
, to the phase of
vector
h, then the value of
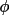 (
h ) is independent of the
enantiomorphous structure. If q(
h ) is significantly
different (modulus
(
h ) is independent of the
enantiomorphous structure. If q(
h ) is significantly
different (modulus
 ) to
) to
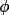 (
h ), then the enantiomorph
may be specified by fixing
(
h ), then the enantiomorph
may be specified by fixing
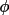 (
h ) at one of its two
possible values.
(
h ) at one of its two
possible values.
For space groups where
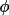 (
h ) is restricted to one of
two values (e.g. for
(
h ) is restricted to one of
two values (e.g. for
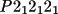
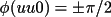 and
and
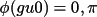 ),
the calculation of q(
h ) from integer set
n' and its application to
the phase set
Q provides a
straightforward approach to identifying the formal
requirements of enantiomorphic discrimination (Hall,
1983).
),
the calculation of q(
h ) from integer set
n' and its application to
the phase set
Q provides a
straightforward approach to identifying the formal
requirements of enantiomorphic discrimination (Hall,
1983).
If all restricted phases have values of
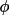 (
h ) = q(
h ), then a reflection with
a non-restricted phase value must be used to specify the
enantiomorph. For these space groups, q(
h ) indicates the range of
values
(
h ) = q(
h ), then a reflection with
a non-restricted phase value must be used to specify the
enantiomorph. For these space groups, q(
h ) indicates the range of
values
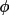 (h) should have to
separate satisfactorily the enantiomorphs. Typically a
(h) should have to
separate satisfactorily the enantiomorphs. Typically a
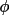 (
h ) value would be permuted
in a multisolution process, to a series of values for q(
h )+
(
h ) value would be permuted
in a multisolution process, to a series of values for q(
h )+
 /4 to q(
h )+3
/4 to q(
h )+3
 /4 in increments of
/4 in increments of
 /4. Differences
between
/4. Differences
between
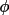 (
h ) and q(
h ) of less than
(
h ) and q(
h ) of less than
 /6 will not provide
strong enantiomorphic discrimination and are likely to lead
to instability in the phasing process. For examples of
enantiomorphic discrimination see Hall (1983).
/6 will not provide
strong enantiomorphic discrimination and are likely to lead
to instability in the phasing process. For examples of
enantiomorphic discrimination see Hall (1983).
In the default mode GENSIN generates both triplet and quartet structure invariant relationships. Invariant types may be specified by the user with the trip and quar control lines. The number of structure invariants generated is determined by a range of parameters, including the number of generators, the magnitude of the E values, and the magnitude of the A and B thresholds. In default mode, the maximum number of invariants for either type is set at 2000.
The reflections used in the generation process are
selected from the largest En, where n designates the
E-type (1 or 2) output by
GENEV
. The default value of n is 1. The number of
generators is controlled by the user via the
gener line, or set
automatically according to the algorithm
MAXGEN = max (10000, 150 + NNHA*(4 + ICNT + 1/NEQP)),
where ICNT=1 if centrosymmetric and ICNT=0 if noncentrosymmetric, NNHA is the number of non-hydrogen atoms in the molecule, and NEQP is the number of general equivalent positions.
Triplet invariants are always generated for up to
100 of the smallest E-values independent of the TRIP
parameters. These are used subsequently in the
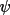 (zero)
figure-of-merit tests in
(zero)
figure-of-merit tests in
GENTAN
, and are referred to as
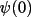 triplets
(Cochran and Douglas, 1957).
triplets
(Cochran and Douglas, 1957).
GENSIN provides, via the
psical line, the
facility to calculate
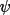 from phases and
structure factor values stored on the bdf. The
from phases and
structure factor values stored on the bdf. The
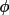 and |F| values on
the bdf may be from a previous
and |F| values on
the bdf may be from a previous
GENTAN
run, an
FC
calculation on a partial structure, or the back
transform of modified density for protein structures. The
bdf
lrrefl:
ID numbers for
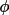 and F are assumed
to be n750 and n751 unless otherwise specified on the
psical line.
and F are assumed
to be n750 and n751 unless otherwise specified on the
psical line.
The inclusion of fragment QPSI values (see the GENSIN line and description above) in the invariant generation process will modify the calculated A and G values, and therefore change the number and nature of invariants generated. This is quite independent of the E used (i.e., E1 or E2). It is recommended that E1, based on random-atom expectation values, are always used, except in special circumstances (see Subramanian and Hall, 1982; Hall and Subramanian, 1982a,b). This is because the QPSI values contain the group structure phase information of the fragment, and E1 has been shown to provide more reliable structure invariant relationships. As a rule-of-thumb E2 should be treated as a second option that the user can invoke in cases of severe non-randomness (e.g., hypersymmetry, super-structures or very dominant heavy atoms).
The
change control line is
available for modifying the magnitude of specific E or
 (E) values.
change can be used to
enhance or to suppress a particular E in the generation
process by increasing or decreasing its E value. It is
also useful for running "replica" tests against other
software and different machines. Please note that
change lines must be
entered in the order of reflection data on the input bdf,
and be the last control lines entered.
(E) values.
change can be used to
enhance or to suppress a particular E in the generation
process by increasing or decreasing its E value. It is
also useful for running "replica" tests against other
software and different machines. Please note that
change lines must be
entered in the order of reflection data on the input bdf,
and be the last control lines entered.
The nature of quartet invariants generated by GENSIN is determined largely by the cross-vector magnitudes. The types and magnitudes of cross-vectors permitted during the generation process are controlled via the parameters IXVF, XVMN, XVMX, XSLO, and XSHI on the quar line. The XSLO and XSHI parameters apply only to quartets with cross-vectors inside the data sphere. The cross-vector limits XVMN and XVMX are applied to individual cross-vector E values. If an individual cross-vector E lies outside the range XVMN to XVMX the quartet is rejected. In the default mode, the sum of the cross-vector magnitudes XVsum (eqn (4.26)) is calculated for all cross-vectors inside the data sphere with XVsum < XSLO and XVsum > XSHI.
Quartets generated by GENSIN are used in several
different ways in the subsequent calculations. Typically
quartets are divided into three categories: those with
cross-vector sums above an upper threshold XSHI (known as
positive quartets), those below a lower threshold XSLO
(known as negative quartets), and those in between. The
last category is often not used in the phasing process
because of the unpredictability of the
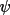
 values. The user can specify these upper and
lower thresholds, XSHI and XSLO, with the
quar line for both the
GENSIN and
values. The user can specify these upper and
lower thresholds, XSHI and XSLO, with the
quar line for both the
GENSIN and
GENTAN
calculations.
It is usual to use only quartets with cross-vectors
inside the data sphere. The XVsum is then able to be
calculated and a prediction made about the value of
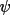
 . There are, however, some drawbacks to this
approach. When XVsum is greater than XSHI it is probable
that the quartet generated will in fact be equivalent to
a combination of three triplet invariants also generated
by the GENSIN process. The phase relationships provided
by positive quartets tend therefore to reinforce, rather
than add to, those provided by the triplets. The phase
"pathways" provided by quartets will, of course, be
different to those of triplets but the generators they
connect will, in effect, be the same.
. There are, however, some drawbacks to this
approach. When XVsum is greater than XSHI it is probable
that the quartet generated will in fact be equivalent to
a combination of three triplet invariants also generated
by the GENSIN process. The phase relationships provided
by positive quartets tend therefore to reinforce, rather
than add to, those provided by the triplets. The phase
"pathways" provided by quartets will, of course, be
different to those of triplets but the generators they
connect will, in effect, be the same.
Quartets with XSLO < XVsum < XSHI are usually not redundant to triplets but are less useful for the reasons already discussed.
Negative quartets with XVSUM less than XSLO provide completely different phase information to triplets but are very few in number. For this reason they are used in GENTAN for a figure-of-merit parameter.
In contrast, quartet invariants with one or more
cross-vectors outside the data sphere, provide
relationships that cannot be represented by a combination
of triplets. These quartets provide new phase pathways
and, as such, could prove crucial in particularly
difficult solutions. The disadvantage of these
"extra-terrestrial" quartets is the lack of cross-vector
information and, therefore, the inability to predict the
value of
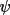
 . However, it may be assumed that
. However, it may be assumed that
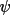
 for these quartets has a distribution based on B
(just as
for these quartets has a distribution based on B
(just as
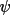
 is a function of A) and an overall reliability
comparable to that of triplets (ignoring the relative
magnitudes of A and B). See Examples 3 and 4.
is a function of A) and an overall reliability
comparable to that of triplets (ignoring the relative
magnitudes of A and B). See Examples 3 and 4.
-
Reads E values from the input archive bdf
-
Writes structure invariant relationships to the file
inv
GENSIN
Generate triplet and quartet invariants to a maximum of 2000 using type-1 E values. Only quartets with cross-vectors inside the data sphere will be output. QPSI values will be applied if fragment information is on the input bdf. Print invariant totals for all generators.
GENSIN nqpi :do not use QPSI information gener *2 300 :use top 300 E values trip yes 1.5 3000 :set max A and max triplets quar no :do not generate quartets print *2 1 50 100 :print SI for gens 1-50 to N of 100
Generate maximum of 3000 triplets with A values greater than 1.5 from 300 generators. Available QPSI values are not applied. Structure invariants for the top 50 generators are printed provided all generator numbers are <= 100.
GENSIN smax .45 :exclude all s values >.45 quar yes 0.75 *8 1. 5. :for Q4 B>.75 and XVsum>5 or <1. change 1 7 3 3.2 :make E = 3.2 change 2 3 -4 2.75 :make E = 2.75
Generate triplets and quartets for generators selected from Es with s<.45. Quartets will be accepted if B>.75 and has a cross-vector sum (all cross-vectors inside the data sphere) 5. or 1. The E value of reflections 1, 7, 3 and 2, 3, -4 will be modified on input.
GENSIN quar *5 outxv :generate quartets with outside cross-vectors
Generate triplets and quartets. The quartets must have at least one of their three cross-vectors outside the data sphere.
GENSIN quar *5 outxv -5. 0. :all cross-vectors outside sphere
Generate triplets and quartets. The quartets must have all three cross-vectors outside the data sphere.
-
Cochran, W. and Douglas, D. 1957. The Use of a High-speed Digital Computer for the Direct Determination of Crystal Structures . Proc. Roy. Soc. A243, 281.
-
Hall, S.R. 1981. A Procedure for Random-access to Reflection Data. J. Appl. Cryst. 14, 214-215.
-
Hall, S.R. 1982. Seminvariant Vectors for Centred Space Groups. Acta Cryst. A38, 874-875.
-
Hall, S.R. 1983. A Procedure for Identifying Enantiomorph-Defining Phases Acta Cryst. A39, 22-26.
-
Hall, S.R. and Subramanian, V. 1982a. Normalized Structure Factors. II. Estimating a Reliable Value of B. Acta. Cryst. A38, 590-598.
-
Hall S.R. and Subramanian, V. 1982b. Normalized Structure Factors. III. Estimation of Errors . Acta Cryst. A38, 598-608.
-
Hauptman, H. 1976. Some Recent Advances in the Probabilistic Theory of the Structure Invariants. Crystallographic Computing Techniques. F.R. Ahmed, K. Huml, B. Sedlacek, eds., Munksgaard. Copenhagen: 129-130.
-
Hauptman, H. and Karle, J. 1956. Structure Invariants and Seminvariants for Noncentrosymmetric Space Groups. Acta. Cryst. 9, 45-55.
-
Karle, J. and Hauptman, H. 1956. Theory of Phase Determination for the Four Types of Non-centrosymmetric Space Groups 1P222, 2P222, 3P12, 3P22. Acta. Cryst. 9, 635-654.
-
Luger, P. 1980 . Modern X-ray Analysis on Single Crystals. de Gruter: New York.
-
Main, P. 1976. Recent Developments in the MULTAN System - The Use of Molecular Structure. Crystallographic Computing Techniques F. R. Ahmed, K. Huml, B. Sedlacek, eds., Munksgaard. Copenhagen: 97-105.
-
Stewart, R.F. and Hall, S.R. 1971. X-ray Diffraction. Determination of Organic Structures by Physical Methods. F.C. Nachod and J.J. Zuckerman, eds., Academic Press: New York, 74-132.
-
Subramanian, V. and Hall, S.R. 1982. Normalized Structure Factors. I. Choice of Scaling Function. Acta. Cryst. A38, 577-590.

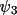
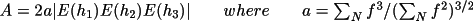
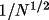
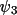
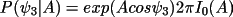
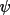

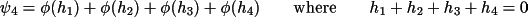
![\[
B = 2 \bm{b} |E( h_{1} ) E( h_{2} ) E( h_{3} ) E( h_{4} )|
\qquad \text{where} \qquad
\bm{b} = \sum _{N}f^{4} / ( \sum _{N}f^{2} ) ^{2}
\]](equations/4.26.1-eq-22.gif)
![\[
P( \psi_{4} |B) = exp(B cos \psi_{4} ) / 2 \pi I_{0} (B)
\]](equations/4.26.1-eq-23.gif)
![\[
P( \psi_{4} |B, E_{12}, E_{13}, E_{14}) = exp(-B cos \psi_{4})/2 \pi I_{0}(Z)
\]](equations/4.26.1-eq-24.gif)
![\[
P( \psi_{4}|B, E_{12}, E_{13}, E_{14}) = exp(-B cos \psi_{4}) / 2 \pi I_{0}(2B)
\]](equations/4.26.1-eq-25.gif)
![\[
XVsum = |E_{12}|+|E_{13}|+|E_{14}|
\]](equations/4.26.1-eq-26.gif)
![\[
< F^{2} (h)> = \sum _{M}G^{2}(h)
\]](equations/4.26.2-eq-27.gif)
![\[
A' = 2a' |E(h_{1}) E(h_{2}) E(h_{3})|
\]](equations/4.26.2.1-eq-28.gif)
![\[
a' = \sum _{M}G(h_{1},h_{2},h_{3}) /
[<F^{2}(h_{1})><F^{2}(h_{2})><F^{2}(h_{3})>]^{1/2}
\]](equations/4.26.2.1-eq-29.gif)
![\[
a'= \sum _{M}[G(h_{1}) G(h_{2}) G(h_{3})] /
[<F^{2}(h_{1})>< F^{2}(h_{2})><F^{2}(h_{3})>] ^{1/2}
\]](equations/4.26.2.1-eq-30.gif)
![\[
B' = 2 \bm{b}'|E(h_{1}) E(h_{2}) E(h_{3}) E(h_{4})|
\]](equations/4.26.2.2-eq-31.gif)
![\[
\bm{b}' = \frac{\sum _{M}[G(h_{1}) G(h_{2}) G(h_{3})G(h_{4})] }
{[<F^{2}(h_{1})><F^{2}(h_{2})><F^{2}
(h_{3})><F^{2}(h_{4})> ]^{1/2}
}
\]](equations/4.26.2.2-eq-32.gif)
![\[
A' = |A'| exp(i \Psi _{3}) \qquad \text{and} \qquad
B' = |B'| exp(i \Psi _{4})
\]](equations/4.26.2.2-eq-33.gif)
![\[
\bm{h}=\sum _{p}n_{j}h_{j}
\]](equations/4.26.3-eq-34.gif)
![\[
\bm{h} = \bm{n} \bm{H}
\]](equations/4.26.3-eq-35.gif)
![\[
\bm{n} = \bm{h} \bm{H}^{-1}
\]](equations/4.26.3-eq-36.gif)
![\[
\bm{u} =\bm{h}'(\mod \bm{m})= (u,v,w)
\]](equations/4.26.3-eq-37.gif)
![\[
\bm{h}' =\Vector{V} \bm{h}
\]](equations/4.26.3-eq-38.gif)
![\[
\bm{U}=(u_{1}, u_{2},. . . . . u_{p})
\]](equations/4.26.3-eq-39.gif)
![\[
|\bm{U}|= +1 \quad \text{or}\quad -1
\]](equations/4.26.3-eq-40.gif)
![\[
\bm{n}' = \bm{n}' \bm{U}^{-1}
\]](equations/4.26.3-eq-41.gif)
![\[
\bm{Q} = (\phi( h_{1}), \phi( h_{2} ), \dots \phi( h_{p} ))
\]](equations/4.26.3-eq-42.gif)
![\[
q(\bm{h}) = \bm{n}' \bm{Q}
\]](equations/4.26.3-eq-43.gif)