Intensity measurements which are negative are generally either excluded from the data set or are reset to zero. Both these practices result in biased determinations of the structure. This bias may be overcome by including all reflections in a refinement based on 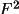. However, for refinements based on F(rel) it is essential to obtain the best possible estimates to the structure factor modulus and its standard deviation.

A more adequate treatment of negative or weak intensities is required. Setting the structure factor to zero ignores the information present in the observation of a negative intensity (i.e. it is weak). Assuming the intensity distribution of data follows the Wilson distribution, and that the true intensity is constrained to be non-negative, a posterior estimate of I or F(rel) and their standard deviations can be made.

When prior information is known, say from a physical model, about an experimental measurement one has a starting point from which to infer a better estimate of the observation from the data. A useful method of employing prior knowledge is in the Bayesian approach to inference where the probability distribution is regarded as a measure of information and represents our degree of belief rather than just relative frequencies. Our interest lies in determining the best estimate of the intensity, denoted J. The experimentally measured intensity I and its variance (I) are subject to counting and statistical error. What must be determined is the probability distribution of J given the observation I. The prior probability distribution of J, p(J), is assumed to be the appropriate Wilson distribution. The likelihood distribution for I, p(I | J), is assumed to be normal with mean J and variance (I). Bayes theorem states that the posterior probability distribution of J given the observation I is:

p(J | I) = k p(J) p(I | J) where p(J) = W(J,Σ) and )

The posterior estimates for I and its esd are given by the following expectation values:

The posterior estimates of F(rel) and (F) may be derived from E(J) and E( (J)) or from the expectation values:

The prior distribution of J assumed requires knowledge of the Wilson parameter, . Assuming the data collected contains a fair number of observations, is determined from the mean value of in shells of (where s=sin / ). The user may specify the number of shells the data is to be divided into through the nrange option in the BAYEST line. The default is 50 shells.

The program searches the bdf for items in a hierarchial manner. The priority item is . If this is present, the distribution of mean versus is calculated and the appropriate values of determined. If I and Lp corrections are found, is generated and the distribution determined. If any of these items are present their esds must also be present.

The user can apply the correction to F(rel) only, leaving the other items as they were input. Otherwise all items present are corrected. The value of F(rel) may be corrected in one of the two following ways.

Note, however, that the two cases are not identical since E(F) does not equal .

The number of shells should be chosen so that there are sufficient reflections in each shell so that a reasonable determination of the distribution may be made (150-200 or reflections per shell).

BAYEST is a two pass operation. The first pass determines the data set distribution and the second pass applies the Bayesian corrections. Items which MUST be present on the bdf are the maximum and minimum values of s, s for each reflection, and either of intensity and Lp, or 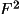. No expansion to the bdf is made. The items input are also output, though the user has the option to apply the correction as desired.

BAYEST nrange 35 frel

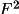In this run the data is divided into 35 groups and the correction is applied to F(rel) only leaving the other items uncorrected. The printing is suppressed. Note that F(rel) and (F) must be present in the input bdf. BAYEST does not expand the bdf by generating F(rel) from I or . That is left to ADDREF.