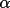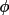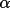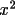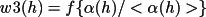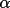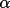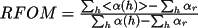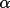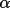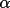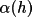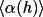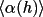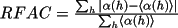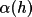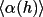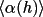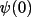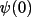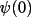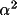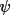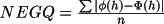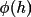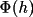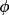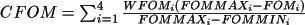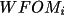|
Author: Syd Hall,
Crystallography Centre, University of Western Australia,
Nedlands WA 6907, Australia
GENTAN uses triplet and/or quartet structure
invariant relationships in a general tangent formula to
propagate and refine structure factor phases. The phases
required to define the cell origin and enantiomorph are
specified automatically, or may be selected (wholly or
partly) by the user.
The tangent formula approach of Karle and Hauptman
(1956) is the most widely used procedure for the extension
and refinement of structure factor phases. Users who are
relatively unfamiliar with this field are well advised to
read summaries of these methods by Karle and Karle (1966)
and Stewart and Hall (1971). Practical guidelines and
background information on the application of the tangent
formula is detailed in the proceedings of the 1975 IUCr
Computing School (Ahmed, 1976).
The tangent formula is a straightforward
computational approach to summing phases estimated with the
triplet invariant relationship
|
(4.44) |
![\[
\psi_{3} = \phi( h_{1} ) + \phi( h_{2} ) + \phi( h_{3} ),
\quad \text{where}\quad
h_{1} + h_{2} + h_{3} = 0
\]](equations/4.27.1-eq-44.gif) |
The conditions for which
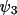 has a value close to zero have been discussed in the
has a value close to zero have been discussed in the
GENSIN
introduction. If there are
m triplet relationships
then the cyclic nature of the contributing phases requires
that the mean value of
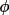 ( (
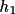 ) has the trigonometric
form ) has the trigonometric
form
|
(4.45) |
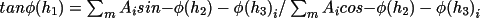 |
Because contributing phases can vary in reliability,
a weighted tangent formula is required to average the
phases as follows,
|
(4.46) |
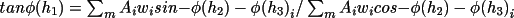 |
The quantity
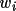 is a measure of the joint
reliability of the two phases contributing to the i'th
triplet invariant. This approach can be applied to any
order of structure invariant. A
general expression for structure
invariants of order
n is is a measure of the joint
reliability of the two phases contributing to the i'th
triplet invariant. This approach can be applied to any
order of structure invariant. A
general expression for structure
invariants of order
n is
|
(4.47) |
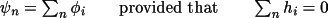 |
It follows from equation (4.46) that the general tangent
formula suitable for application to these invariants has
the form shown in equation (4.48) (Hall, 1978). X is A, B, . . .
according to the order of the invariant.
|
(4.48) |
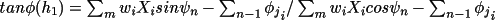 |
The general tangent formula also permits the use of
non-zero
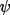 values. This is
particularly important if oriented or positioned fragment
information is used to estimate values. This is
particularly important if oriented or positioned fragment
information is used to estimate
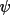 from the group
structure factors (see the from the group
structure factors (see the
GENEV
and
GENSIN
documentation and the section on partial structure
information below). In strongly non-random structures
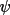 can depart
significantly from zero even for invariants with large X
values. can depart
significantly from zero even for invariants with large X
values.
It has also been discussed in GENSIN that
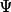 may be expected to
be closer to may be expected to
be closer to
 than 0 for negative
quartets (see the than 0 for negative
quartets (see the
GENSIN
documentation for definition). The negative quartets
are used by GENTAN for FOM purposes only, unless the
active
option is entered on the
invar line (then negative
quartets are used actively and
not for the FOM).
Starting the tangent processThe tangent phasing process is usually initiated with
a few "known" phases. From these phases additional values
are determined through the application of the tangent
formula to connecting invariant relationships. In turn, new
phases are used to expand the phasing process
further.
The tangent refinement of a phase set stops when the
estimated phases converge to a constant
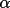
 value. Convergence occurs when the refined phases
are self-consistent with the structure invariant
relationships and the refinement constraints applied (e.g.,
weighting scheme). Due to the pyramidal nature of the
phasing process (i.e., a few phases determine many), the
final phase set is also strongly dependent on the starting
phases. To a large extent the success or failure of the
multisolution method is determined by the actual values of
the starting phases. This is why a great deal of the
computational effort goes into the selection of starting
reflections. value. Convergence occurs when the refined phases
are self-consistent with the structure invariant
relationships and the refinement constraints applied (e.g.,
weighting scheme). Due to the pyramidal nature of the
phasing process (i.e., a few phases determine many), the
final phase set is also strongly dependent on the starting
phases. To a large extent the success or failure of the
multisolution method is determined by the actual values of
the starting phases. This is why a great deal of the
computational effort goes into the selection of starting
reflections.
Where do the "known" starting phases come from? Some
may be specified directly in order to fix the origin in the
cell. These are known as origin defining reflections (ODR).
ODR phases alone are usually insufficient to reliably start
the phasing process. The larger the number of starting
phases, the less dependence there is on the reliability of
a few invariant relationships and the higher the likelihood
of obtaining a correct solution.
Where do the additional "known" phases come from?
Because phase values are usually not known before a
solution, one way is to assign trial phase values to a
limited number of reflections and permute these in a series
of separate tangent refinements. Permuted starting phases
form the basis for the multisolution approach to the
tangent phasing process.
Selecting Origin Defining Reflections
(ODR)The first step in the GENTAN calculation is to
specify sufficient phases to define uniquely the cell
origin. The formal conditions required to do this have
been detailed in the GENSIN documentation. The
specification of phases to fix the cell origin is to be
done automatically unless the user intervenes via the
phi or
assign control lines.
All ODR phases entered are checked for validity by the
program. If they are incorrect or insufficient,
additional or new phases will be automatically selected
to satisfy the origin fixing requirements.
permute and
magic : Selecting
starting phasesThe selection of starting phases which are involved
in reliable structure invariant relationships is critical
to the success of these methods. In GENTAN, the generator
reflections are sorted by a convergence-type process
(Woolfson, 1976) that maximizes the connections through
structure invariant relationships between ODR phases and
additional starting phases. This is called the
MAXCON(nection) procedure. If the structure is
noncentrosymmetric this procedure is also used to specify
one or more EDR (enantiomorph defining reflection) phases
to fix the enantiomorphic form of the structure. This is
done automatically by the MAXCON procedure unless the EDR
phase is selected manually by the user. Additional phases
are specified in the MAXCON procedure as requested (see
field 2,
select line). The
MAXCON procedure sorts generator reflections in order of
descending connectivity and this sort order is used in
all subsequent operations. The sorted order of generators
is referred to as the phase path. The origin,
enantiomorph, and any other MAXCON-selected phases are at
the beginning of this path.
In addition to the starting phases selected for
maximum connectivity, phases are specified to optimize
the rate of "phase extension" to the remaining
generators. This is referred to as the MAXEXT(ension)
procedure. Extra phases are often needed in the starting
set to accelerate phase propagation along the sorted
phase path, rather than maximizing the connections
between the initial starting set. It is important to
emphasise that the MAXCON approach insures that there are
strong links between the initial starting set and other
strong generators, while the MAXEXT procedure provides
additional phases which enhance the rate at which new
phases are generated in one pass down the phase path. The
criteria used in the MAXEXT procedure to measure the rate
of "phases extension" is specified in field 6 of the
select control
line.
Both the MAXCON and MAXEXT procedures use all
available triplet and quartet invariant relationships
unless instructed otherwise (see field 5,
select line). This
option is useful if the automatically selected starting
phases fail to provide a solution. Note that field 1 of
the
invar line has
precedence over this option.
The permutation of phases assigned to starting
reflections is performed in several ways. In the
perm
ute mode (see field 1,
select line), each
starting phase (other than the ODRs) is assigned a value
according to whether it is restricted or unrestricted.
Restricted phases can have two values (separated by
 ) and unrestricted
phases are usually assigned four different values
(separated by ) and unrestricted
phases are usually assigned four different values
(separated by
 /2). In this mode
therefore, the total number of phase sets tested is
increased by a factor of two, or four, for each
restricted, or unrestricted, phase specified. The number
of phase sets increases very rapidly with the number of
unrestricted starting phases. /2). In this mode
therefore, the total number of phase sets tested is
increased by a factor of two, or four, for each
restricted, or unrestricted, phase specified. The number
of phase sets increases very rapidly with the number of
unrestricted starting phases.
An alternative approach to phase permutation is
available using the magic integer procedure of White and
Woolfson (1975). The
magic
option (field 1,
select line) permutes
the unrestricted starting phases so that the number of
phase sets increases at a much lower rate. If a large
number of unrestricted phases is needed to start an
analysis, the magic integer permutation approach can
provide a considerable reduction in computing time. The
magic
permutation procedure does increase the
initial rms error of phases but for large analyses this
is is usually a worthwhile tradeoff for benefits of more
unrestricted starting phases.
random : Specifying
random starting phasesThe inherent fragility of a phasing process started
with a limited set of known phases and extended
sequentially to all other phases has already been
discussed. The success of this procedure hinges on the
reliability of a few individual structure invariants.
This is particularly critical in the early stages of the
extension process when new phase estimates are often
determined from one or two relationships. An incorrect
phase estimate at this stage will frequently cause the
phasing procedure to fail.
The random phase approach of Yao Jia-xing (1981) is
an alternative to using a limited set of permuted phases.
In the
random
mode (field 1,
select line) random
phases are assigned to all generators except the origin
defining reflections. The use of random starting phases
lessens the dependence on a small number of critical
relationships by insuring that all invariants are
immediately involved in the phase refinement process.
Weights of each refined phase are used to filter the
phase extension process. When the weight w(h) of phase
estimate
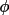 (h) exceeds its
starting value (default is 0.25 - see field 9,
select line), this
phase replaces the random starting value. This mode is
particularly useful for large structures in low symmetry
where there are few relationships among generators, and
for strongly non-random structures where invariant
relationships with large probability factors may still be
suspect. Strong enantiomorph definition is also possible
through the application of random starting phases. (h) exceeds its
starting value (default is 0.25 - see field 9,
select line), this
phase replaces the random starting value. This mode is
particularly useful for large structures in low symmetry
where there are few relationships among generators, and
for strongly non-random structures where invariant
relationships with large probability factors may still be
suspect. Strong enantiomorph definition is also possible
through the application of random starting phases.
In the
random
start mode, tangent refinements are
performed on different random starting sets until either
a correct solution is identified, or the phase set
maximum is reached. The user may specify a random number
generator "seed" (field 10,
select line) and in
this way insure that repeat runs employ different random
starting phases. Alternatively, the default seed will
insure that the same random phases will be generated, if
this procedure is desired in a re-run.
Tangent phase extension and refinementThe extension and refinement of phases is
simultaneous in the tangent process. When a structure
invariant relationship contains only one unknown phase then
this phase is estimated from the relationship. This is
referred to as a phase extension. If all phases in an
invariant are known, then each member phase is determined
by a combination of the others. When a phase occurs in more
than one such invariant, the estimate of its value is
averaged or refined. Repeated averaging of phases in this
way is referred to as phase refinement. As discussed
earlier, the generator reflections and related invariants
are sorted into an optimal phase path during the selection
of starting phases. Reflections and invariants are
subsequently processed in this sequence and one pass down
this list is known as a single refinement iteration. The
maximum number of refinement iterations may be specified by
the user via the
refine control line
(field 3). The default value is 30.
The reliability of each phase estimate
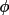 (h) is gauged by
the calculated value of (h) is gauged by
the calculated value of
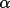 (h) (see equation
(4.52) below). Phases are accepted for phase extension if the
value of (h) (see equation
(4.52) below). Phases are accepted for phase extension if the
value of
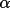
 (h) is above a threshold (see field 5,
refine line). This
threshold is reduced with each iteration (see field 7) thus
insuring that the most reliable phases are used in the
early iterations. (h) is above a threshold (see field 5,
refine line). This
threshold is reduced with each iteration (see field 7) thus
insuring that the most reliable phases are used in the
early iterations.
Only the top sorted generators (those used in the
MAXEXT selection process (see field 4,
select line)) are phased
in the early iterations. When the average value of
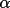
 (h) changes less than a specified percentage (see
field 7,
refine line) additional
generators (50, or 25% of total, whichever is greater) are
added to the phasing process. The weight of each phase, is
also used to control phase extension and refinement. A
weight threshold is set for the duration of the refinement
(see field 4,
refine line) and is used
to reject less reliable phases. (h) changes less than a specified percentage (see
field 7,
refine line) additional
generators (50, or 25% of total, whichever is greater) are
added to the phasing process. The weight of each phase, is
also used to control phase extension and refinement. A
weight threshold is set for the duration of the refinement
(see field 4,
refine line) and is used
to reject less reliable phases.
There are two different methods for propagating
phases in GENTAN;
cascade
and
block
. These two modes differ only in the point in
the tangent iteration where the phase is estimated. The
difference in procedure can, however, have a profound
effect on phase convergence and stability.
block : Phase
estimation AFTER a tangent iterationThe
block
procedure differs from the
cascade
method in that known phase values remain
fixed during a tangent iteration. New phase estimates are
only calculated at the completion of an iteration. This
insures that phase estimates are made from fixed phase
values, and the
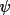 values of
invariants remain constant for the entire iteration.
Phases are therefore determined as a block defined by the
current length of the phase path. This procedure will not
propagate phases as rapidly as the values of
invariants remain constant for the entire iteration.
Phases are therefore determined as a block defined by the
current length of the phase path. This procedure will not
propagate phases as rapidly as the
cascade
mode but it is less susceptible to phase
instability when values of
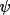 depart
significantly from zero. It is the recommended procedure
for strongly non-random structures. depart
significantly from zero. It is the recommended procedure
for strongly non-random structures.
The tangent formula weight is defined by the joint
probabilities of the phases contributing to the RHS of
equation (4.48). If the individual weight of a phase is
defined as
|
(4.49) |
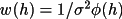 |
and the joint tangent weight as
|
(4.50) |
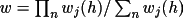 |
The variance of an unrestricted phase
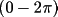 is given by the
following expression (Karle and Karle, 1966) where is given by the
following expression (Karle and Karle, 1966) where
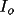 and and
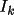 are modified Bessel
functions dependent on are modified Bessel
functions dependent on
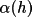 , ,
|
(4.51) |
![\(
\sigma ^{2}\phi (h) = \pi ^{2}/3 +
4/I_{o}\sum _{inf}[(-1) ^{k}I_{k}/k^{2}]
\)](equations/4.27.4-eq-51.gif) |
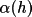 is a measure
of agreement between contributing estimates of is a measure
of agreement between contributing estimates of
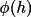 within the
tangent formula and is defined in the following equation
where T and B are the tangent formula numerator (top) and
denominator (bottom), respectively: within the
tangent formula and is defined in the following equation
where T and B are the tangent formula numerator (top) and
denominator (bottom), respectively:
|
(4.52) |
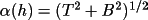 |
It follows that the variance of
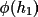 may be calculated from
equations (4.51) and (4.52).
Computationally, however, this is
prohibitive so in practice it is necessary to approximate
w(h). GENTAN provides for three different weighting
schemes: probabilistic, Hull-Irwin statistical, and
modified statistical.
may be calculated from
equations (4.51) and (4.52).
Computationally, however, this is
prohibitive so in practice it is necessary to approximate
w(h). GENTAN provides for three different weighting
schemes: probabilistic, Hull-Irwin statistical, and
modified statistical.
w1 : Probabilistic
weightsFor unrestricted phases the weight w(h) based on
equation (4.51) is approximately linear with respect to
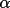 (h) (see p92-94,
Stewart and Hall, 1971). It is possible, therefore, to
approximate w(h) as K (h) (see p92-94,
Stewart and Hall, 1971). It is possible, therefore, to
approximate w(h) as K
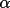 (h) where K is
set a fixed fraction. This approach has the disadvantage,
however, of not providing weights normalized about 1.0.
This normalization is important for the correct
evaluation of (h) where K is
set a fixed fraction. This approach has the disadvantage,
however, of not providing weights normalized about 1.0.
This normalization is important for the correct
evaluation of
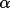 (h) from
equation (4.52). In addition, for very large structures, all (h) from
equation (4.52). In addition, for very large structures, all
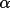 (h) values will
be small and weights based only on (h) values will
be small and weights based only on
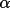 (h) alone must
also be small. The converse is true for small structures.
For this reason, GENTAN uses a modified probabilistic
weight which is essentially structure-independent and has
values restrained to the range of 0 to 1. (h) alone must
also be small. The converse is true for small structures.
For this reason, GENTAN uses a modified probabilistic
weight which is essentially structure-independent and has
values restrained to the range of 0 to 1.
|
(4.53) |
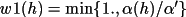 |
where
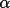 ' = min ( 5.,
X ) and X is mean A (triplet) or B (quartet). ' = min ( 5.,
X ) and X is mean A (triplet) or B (quartet).
The value of w(h) calculated from equation (4.51) is
not valid for restricted phases because it assumes a
continuous phase distribution. For restricted phases
the probability that cos
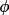 (h) is positive
is given by the following expression: (h) is positive
is given by the following expression:
|
(4.54) |
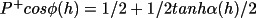 |
It follows that weight of an individual phase has the form
|
(4.55) |
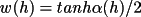 |
Although w(h) calculated from equation (4.55) will
lie in the range 0.0 to 1.0, it has the same
deficiencies of unrestricted weights based solely on
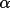 (h). For this
reason GENTAN uses the relative weight expression for
restricted phases. (h). For this
reason GENTAN uses the relative weight expression for
restricted phases.
|
(4.56) |
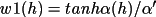 |
where
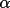 ' = min(2., X)
and X = mean of A (triplets) or B (quartets) ' = min(2., X)
and X = mean of A (triplets) or B (quartets)
w2 : Hull-Irwin
Statistical WeightsThe probabilistic weight
w1
is not suitable for application to some
structural types. It tends to increase rapidly to 1.0
even for a small number of invariant relationships. As a
consequence, it can be insensitive to significant
variations in phase agreement. In addition, the
w1
weighting scheme has no provision for
over-correlated phase sets which are characterized by
unexpectedly high
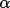 (h)
values. (h)
values.
To overcome these deficiencies, Hull and Irwin
(1978) have suggested a weighting scheme based on the
ratio of
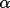 (h) and the
expectation value < (h) and the
expectation value <
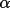 (h)>. It has
the general functional form (h)>. It has
the general functional form
|
(4.57) |
![\(
w2(h) = f { [\alpha (h) / <\alpha (h)>]^{2}}
\)](equations/4.27.4.2-eq-57.gif) |
|
(4.58) |
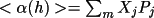 |
where
|
(4.59) |
 |
|
(4.60) |
 |
The precise functional form of
![\(f[] \)](equations/4.27.4.2-inl-1046.gif) is given by
Hull and Irwin. is given by
Hull and Irwin.
The w2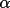 (h)>
calculated from the actual number of invariants involved
in the current estimate of (h)>
calculated from the actual number of invariants involved
in the current estimate of
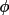 (h). Secondly,
the value of weight (h). Secondly,
the value of weight
w2
decreases if the phase agreement exceeds
that expected for that stage of the refinement. In this
way, it reduces the contribution of over-correlated phase
estimates and enhances values that are close to that
expected. Thirdly,
w2
takes into account the importance of phase
correlation effects to weighting for different structure
analyses (see the plot of
w2
above). At the same time the overall
magnitude of
w2
is essentially independent of structure
size, and the scaling procedures used in
w1
are not needed.
There is, however, a fundamental limitation to
w2
which is due to its implicit dependence on
a reliable estimate of the
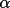 expectation
value. For strongly non-random structures the estimates
for < expectation
value. For strongly non-random structures the estimates
for <
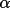 (h)>, based
on equations (4.59) and (4.60), may be inaccurate and this
can lead to incorrect weights. In these cases the (h)>, based
on equations (4.59) and (4.60), may be inaccurate and this
can lead to incorrect weights. In these cases the
w1
weights, which are based solely on phase
agreement (i.e.,
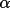 (h)), will tend
to be more reliable. (h)), will tend
to be more reliable.
w3 : Modified H-I
Statistical WeightsThis weighting scheme is identical to
w2
except that it is a function of x rather
than
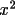 . That is, . That is,
|
(4.61) |
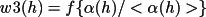 |
w3w2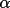 (h) and < (h) and <
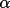 (h)>. In some
structures this is advantageous, particularly when
invariant relationships are sparse and there is a
tendency for phase oscillations. The weights due to (h)>. In some
structures this is advantageous, particularly when
invariant relationships are sparse and there is a
tendency for phase oscillations. The weights due to
w3w2w1w3w1w2
Identifying the correct phase setIt is very desirable in multisolution tangent methods
to have some method of detecting "correct" phase sets prior
to computing a Fourier transform (i.e., E-map). An a priori
assessment of phase sets is made in GENTAN using two
'measure of success' parameters CFOM and AMOS. These
parameters are based principally on the four
figures-of-merit, RFOM, RFAC, PSI0, and NEGQ.
Combined Figure-of-Merit (CFOM)The combined FOM is a scaled sum of the four FOM
parameters RFOM, RFAC, PSI0 and NEGQ.
|
(4.66) |
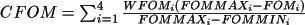 |
The FOM weights
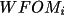 may be specified on the
setfom control line.
These values are subsequently scaled so that the maximum
value of CFOM is 1.0. It is important to stress that CFOM
is a relative parameter and serves mainly to highlight
which is the best combination of FOMs for a given run. It
does not indicate whether these FOMs will provide a
solution. may be specified on the
setfom control line.
These values are subsequently scaled so that the maximum
value of CFOM is 1.0. It is important to stress that CFOM
is a relative parameter and serves mainly to highlight
which is the best combination of FOMs for a given run. It
does not indicate whether these FOMs will provide a
solution.
Absolute Measure-of-Success Parameter
(AMOS)The AMOS parameter is a structure-independent gauge
of the correctness of a phase set. It uses pre-defined
estimates of the optimal values for the FOM parameters
RFOM, RFAC, PSI0 and NEGQ. OPTFOM values may be user
defined (see
setfom line). Rejection
values for the four FOM parameters are derived from the
OPTFOM values as REJFOM=2*OPTFOM. The default values are
as follows,
The absolute measure-of-success parameter
is calculated from all active FOMs as
|
(4.67) |
 |
where the WFOM values are scaled so that AMOS
ranges from 0 to 100. In addition to being used to sort
phase sets in order of correctness, the AMOS values
provide a realistic gauge of the correctness of phase
sets. As a rule of thumb, AMOS values can be interpreted
in the following way:
These classifications are only approximations. The
predictability of optimal FOM values can be perturbed by
a variety of structure dependent factors and by the FOM
weighting. Nevertheless, the AMOS value provides the user
with a concise overview of the phase sets.
Phase sets must satisfy certain criteria before being
considered for possible output to the bdf. Each phase set
is tested at three stages in the tangent process and is
rejected if the FOM values and other parameters are outside
acceptable limits. In this way time is not spent on phase
sets that have little or no chance of being correct - a
very desirable feature for a multisolution
procedure.
The first rejection test is made following the sixth
tangent iteration and involves only the top block of sorted
phase estimates. This is referred to as the PRETEST of FOMs
and the rejection criteria 011, 012, and 014 are applied.
The user may disable the PRETEST of FOMs with the
setfom line (field 1).
The second rejection test is made after the last tangent
iteration and a phase set is rejected according to the
criteria 021, 022, 023, 024, and 025. The final rejection
test occurs during the sorting of phase sets and the
calculation of the AMOS value. Phase sets are rejected if
criteria 036 and 037 are not satisfied.
PRETEST Rejection
Criteria
Last Iteration Rejection
Criteria
Final Rejection Criteria
Tests for phase correctness are made at the same time
as the second rejection test. These are made on the basis
of the optimum FOM values, OPTFOM. If all tests are
satisfied, the tangent phasing process is terminated and
the program enters the sort mode. In this way GENTAN
insures that computing time is not wasted on generating
further phase sets when a correct set of phases has already
been calculated. This is particularly important when the
random
start option is invoked. Tangent cycling is
terminated
if RFOM
< OPTFOM(1) and RFAC < OPTFOM(2) and PSI0 <
OPTFOM(3) and NEGQ < OPTFOM(4) and av. φ >
45° If inadvertant termination occurs, the user can
adjust the OPTFOM values used in the above criteria, or
switch off this test entirely (field 10,
setfom line).
Application Of Partial Structure Data
Psi Calculated from Fragment InformationIf structure information of types 3 and 4 (oriented
and positioned) is entered into the GENEV calculation,
and the
qpsi
option is invoked in GENSIN, then the phase
estimate of the invariant may be used in the extension
and refinement process. This can provide a significant
improvement to the phasing process, particularly for
planar and heavy-atom structures, and provides a valuable
second line of attack for less tractable problems. The
rule of thumb is: "if oriented or positional structural
information is available, use it!"
Applying Structure Factor Phases as Starting
PhasesAn alternative approach to partial structure
information is to use calculated structure factor phases
as input starting phases (Karle, 1976). This approach has
the advantage over the group structure factor method of
not requiring the repeat of
GENEV
and
GENSIN
calculations. In practice this method is limited
because it fails to take into account the expected change
to the
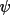 values which is
available from knowledge of the structure. Because of
this, strongly non-random structural features tend to
dominate the phases. Nevertheless, careful application of
the parameters on the
partsf line can provide
an important alternative to applying known structural
information. values which is
available from knowledge of the structure. Because of
this, strongly non-random structural features tend to
dominate the phases. Nevertheless, careful application of
the parameters on the
partsf line can provide
an important alternative to applying known structural
information.
-
Reads |E| values from input archive bdf
-
Writes estimated phases to the output archive
bdf
-
Reads structure invariants from file
inv
This run automatically selects starting phases.
Phases are extended and refined in the
block
mode using weight scheme 2. The top four
phase sets are written to the output bdf. All FOM rejection
and cycle termination tests will be applied.
-
Ahmed, F.R. and Hall, S.R. 1976.
Computer Application of the Symbolic
Addition and Tangent Procedure.
Crystallographic Computing Techniques, Eds. F.R.
Ahmed, K. Huml, B. Sedlacek Munksgaard: Copenhagen,
71-84.
-
Cochran, W. and Douglas, A.S. 1955.
The Use of a High Speed Digital Computer
for the Direct Determination of Crystal Structures
I. Proc. Roy. Soc., A277, 486-500.
-
Hall, S.R. 1978. Paper 15.1-2,
Collected Abstracts. 11th IUCr
Congress, Warsaw.
-
Hull, S.E. and Irwin, M.J. 1978.
On the Application of Phase Relationships
to Complex Structures.
XIV. The Additional Use of Statistical
Information in Tangent-Formula Refinement.
Acta Cryst.,
A34, 863-870.
-
Karle, J. 1976.
Structures and Use of the Tangent Formula
and Translation Functions.
Crystallographic Computing Techniques. Eds. F.R.
Ahmed, K. Huml, B. Sedlacek. Munksgaard: Copenhagen,
155-164.
-
Karle, J. and Hauptman, H. 1956.
Theory of Phase Determination for the Four
Types of Non-Centrosymmetric Space Groups 1P222,
2P222, 3P12, 3P22. Acta Cryst.,
9, 635.
-
Karle, J. and Karle, I.L. 1966.
The Symbolic Addition Procedure for Phase
Determination for Centrosymmetric and
Noncentrosymmetric Crystals. Acta Cryst.,
21, 849.
-
Main, P., Fiske, S.J., Hull, S.E., Lessinger,
L., Germain, G., Declercq, J.P. and Woolfson, M.M.
1980.
MULTAN-80 Program Writeup, Dept.
of Physics, University of York, York, England.
-
Stewart, R.F. and Hall, S.R. 1971.
X-ray Diffraction: Determination of Organic
Structures by Physical Methods. Eds. F.C.
Nachod and J.J. Zuckerman. Academic Press: New York,
74-132.
-
White, P.S. and Woolfson, M.M. 1975.
The Application of Phase Relationships to
Complex Structures VII. Magic Integers,
Acta Cryst.,
A31, 53-56.
-
Woolfson, M.M. 1976.
Doing Without Symbols - MULTAN.
Crystallographic Computing Techniques. Eds. F.R.
Ahmed, K. Huml, B. Sedlacek.Munksgaard: Copenhagen,
85-96.
-
Yao Jai-xing. 1981.
On the Application of Phase Relationships
to Complex Structures XVIII. RANTAN - Random
MULTAN, Acta Cryst.,
A37, 642-644.
|
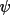 values which is
available from knowledge of the structure. Because of
this, strongly non-random structural features tend to
dominate the phases. Nevertheless, careful application of
the parameters on the
partsf line can provide
an important alternative to applying known structural
information.
values which is
available from knowledge of the structure. Because of
this, strongly non-random structural features tend to
dominate the phases. Nevertheless, careful application of
the parameters on the
partsf line can provide
an important alternative to applying known structural
information.![\[
\psi_{3} = \phi( h_{1} ) + \phi( h_{2} ) + \phi( h_{3} ),
\quad \text{where}\quad
h_{1} + h_{2} + h_{3} = 0
\]](equations/4.27.1-eq-44.gif)
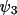
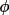
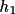
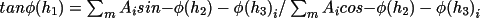
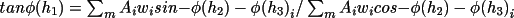
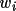
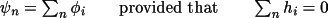
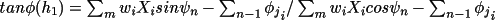
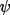
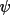
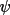
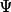

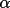



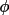
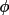
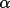
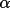

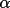

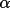

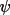
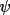
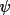
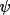
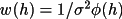
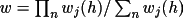
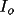
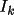
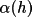
![\(
\sigma ^{2}\phi (h) = \pi ^{2}/3 +
4/I_{o}\sum _{inf}[(-1) ^{k}I_{k}/k^{2}]
\)](equations/4.27.4-eq-51.gif)
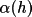
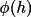
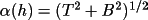
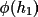
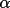
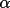
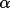
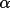
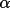
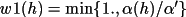
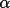
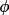
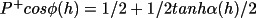
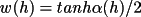
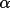
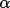
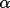
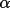
![\(
w2(h) = f { [\alpha (h) / <\alpha (h)>]^{2}}
\)](equations/4.27.4.2-eq-57.gif)
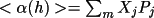


![\(f[] \)](equations/4.27.4.2-inl-1046.gif)