PATSEE
: Search for molecular fragment
Authors: Ernst Egert and Syd
Hall
Contact: Ernst Egert,
Institut für Organische Chemie, Universität
Frankfurt, Niederurseler Hang, D-6000 Frankfurt am Main,
FRG.
PATSEE searches for a fragment of known geometry
in the unit cell using an integrated Patterson and direct
methods procedure. This program, which is valid and
efficient for all space groups, is based on the standalone
program written by Ernst Egert for the SHELX system. The
rotation search is applicable to a fragment of any size and
allows one torsional degree of freedom. The translation
search may locate up to two independent search models of
any size (including single atoms), taking into account
known atoms at fixed positions, if any. The principles of
this method are detailed by Egert & Sheldrick (1985),
Acta Cryst. A41, 262-268.
The choice of strategy for the solution of a crystal
structure at atomic resolution is usually determined by the
presence or absence of heavy atoms. Thus it is common
practice to solve light-atom structures with direct methods
and those containing heavy atoms with Patterson techniques.
If thisstrategy fails, it may be advisable to resort to the
corresponding alternative method; direct methods may well
reveal the positions of heavy atoms, and the Patterson
function can be interpreted even for purely light-atom
structures, such as those of organic molecules, provided
that part of the molecular geometry is known. This
so-called Patterson search has been shown by various
authors to be a powerful tool for solving difficult crystal
structures; its great strength is that it employs chemical
information directly, and so can compensate for mediocre
precision and resolution of the X-ray data. PATSEE combines
the merits of both Patterson and direct methods - in a
manner that is generally applicable, efficient, automatic
and easy to use - and thus to exploit all the
a priori available information in order
to solve large problem structures.
Preparation of the Search
Generally, a Patterson search in vector space
consists of the following stages: (1) definition of a
search model; (2) calculation and storage of the Patterson
function; (3) rotation search, and (4) translation search.
It is a serial technique, with the last two stages
crucially dependent on the accuracy of the preceding ones.
Thus the first step is by no means trivial; this is
especially true for a procedure such as this where the
fragments are taken as rigid and no model refinement is
attempted (with the exception of one torsional degree of
freedom between rigid groups). Usually a small well-defined
search model is more appropriate than a larger one
containing several incorrect atoms. The model is defined by
atomic coordinates in a given coordinate system; these will
normally be either fractional (taken from a related crystal
structure) or Cartesian (e.g. from a force-field
calculation).
The triplet structure invariant relationships which
are required for the translation search (if applied) are
calculated prior to the PATSEE run using
GENSIN
(which gets its E-values from
GENEV
). The
lac1.dat
example given below shows a typical input
sequence for the
GENEV
,
GENSIN
,
FOURR
FOURR, PATSEE calculations. Note that
lac1 is one of the Xtal
test decks so that reference to the
lac1 listing will be useful
in guiding initial PATSEE applications.
The Patterson map is generated by the program
FOURR
. For almost all purposes, we recommend using E.F as
the coefficient (
epat
full
); these lead to a sharper map than
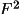 (
(
patt
full
) but generate fewer ripples than
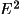 -1 (
-1 (
vect
full
).
The region around the origin of the Patterson
function is dominated by
intra- molecular vectors, which depend
on the orientation but
not on the position of the fragment.
Thus the full six-dimensional search can be split into two
three-dimensional searches, a
rotation and a
translation search (depending on the
space group, the latter may be of even lower
dimensionality).
The atom fragment information used in the searches is
entered in the following way. Atom site coordinates may be
entered as fractional or Cartesian according to the option
on the preceding
FRAG line. Each group of
atom sites must be preceded by a
FRAG line, or in the case
of sites loaded from the bdf, the
FRAG line(s) contain the
labels of the atom sites to be used in the search. The
position of each fragment of the atom sites in the input
stream determines how they are used in PATSEE. A fragment
that precedes the
rotate line will be
fixed (i.e. the vectors between these
atoms will be neither rotated nor translated but they will
be used in the figure of merit calculations). Fragment(s)
that follow the
rotate line but precede
the
transl line will be
rotated and translated. Fragments that
follow the
transl line will be
translated only. The
shift,
spin and
twist lines are used
modified the atom sites in a fragment. If a
shift or a
spin line will transform
or rotate, respectively, the atom sites of the
next fragment. The
twist line serves a
different function -- it enables two parts of a fragment to
be rotated about a connecting bond (and searches are
applied for each twist settings). The
twist line must be
positioned in the input stream between the two atom sites
which will be twisted with respect to each other.
The first step in the rotation search is to set up
the
intra -molecular vector set to be used
for the search, i.e. to express the model geometry (which
should always be checked thoroughly - see the
geom
option on the
PATSEE line) in the form
of discrete vectors with associated weights. Of the
N(N-1)/2 intramolecular vectors, the short (e.g. d<
p
Å, see
vlim
) and long (e.g. d >
q
Å, see
vlim
) values are immediately eliminated. Since
the inner sphere around the Patterson origin shows some
vector density everywhere, the short vectors provide little
angular discrimination and are normally not very useful for
determining the orientation of the fragment. However, they
may be important for molecules (e.g. those consisting of
fused aromatic rings) that are characterized by a few short
vectors with high weights. An upper limit for the vector
length is also advisable because very long vectors, though
quite characteristic of the search model, suffer most from
uncertainties in the geometry and could easily miss the
corresponding maximum in the Patterson map. Close vectors
(see
vres
) are replaced by a weighted average vector
with the combined weight. In order to save computing time,
low-weight vectors may be omitted from the figure of merit
assessment (see
vfom
).
Any orientation of a rigid fragment relative to a
fixed coordinate system can be described by three angles
corresponding to successive rotations about properly chosen
axes. (There are various definitions of the Eulerian
angles. For computational reasons, we prefer successive
rotations about the
a,
b and
c axes, in that order.) The asymmetric
unit of angular space depends on both the Laue group and
the model symmetry. Instead of scanning the respective
range of angles by specifying rotation increments, we have
chosen to generate random orientations (see
nran
). The optimum number of orientations (see
ntry
) to be tried depends on the size and the
shape of the search fragment, the Laue group and the
Patterson grid intervals. PATSEE usually generates
10000-600000 angle triplets, which corresponds to mean
rotation increments of about 7°; this is normally
sufficient for the coarse location of the maxima.
For each orientation, the correlation between the
rotated intramolecular vector set and the Patterson
function is measured by a
product function (note that this is a
different approach to non-Xtal versions of PATSEE). The
weight of each vector
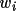 is thus multiplied with the nearest Patterson
grid value
is thus multiplied with the nearest Patterson
grid value
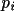 . The rotation figure of merit (
Rfom ) is ?
. The rotation figure of merit (
Rfom ) is ?
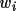
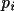 for a specified sample (see fraction
for a specified sample (see fraction
f
of
vfom
) of the largest weighted vectors. Note that
these vectors are sorted into a test list in the order of
descending
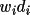 values, where
values, where
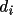 is the vector length.This
is important because a pretest requires that the top
is the vector length.This
is important because a pretest requires that the top
t
(see
vtes
) of the vector list has a
Rfom which is positive or the
orientation is immediately rejected. The sorting is
necessary to avoid the dominance of this test by short
heavily weighted vectors. If the final normalized
Rfom is <
p
(see
fomt
) the orientation is also rejected.
Before an orientation is placed in the short list of
best solutions, it must pass two tests. The 'overlap test'
ensure that no close interatomic contacts arise form the
application of the lattice translations present and the
'equivalence test' compares the orientation in question
with those already stored. Two orientations are regarded as
similar when all pairs of equivalent atoms are close to
each other; in that case only the better one is
kept.
In order to improve the performance of the subsequent
translation search, the best solutions are 'refined' by a
restricted and finer rotation search. The maximum within
each promising region of angular space is found by testing
up to
n
(see
nref
) additional random points, which corresponds
to a mean rotation increment of less than
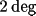 .
.
Users may also specify the starting orientation of a
fragment (see
seta
) and the range or the random rotations (see
setr
). This is normally only used, however, if a
rotation search is repeated over a target set of
orientations.
If the search model has one torsional degree of
freedom the rotation searches are repeated for each
distinct geometry using the
twist option. This
specified by a range of possible torsion angles and an
appropriate increment. Invocation of
twist causes a merged
list of best solutions is set up. At the end of the
rotation search, a small number of promising orientations
are passed over to the translation search. It is our
experience that the correct one is usually present among
the best two or three for reasonably sized
fragments.
TRANSL-
Translation Search
In procedures to position a fragment of known
geometry in the unit cell, the translation search has
usually proved to be less reliable than the rotation
search. This is because the 'cross' (i.e.
inter -molecular) vectors used to
locate a fragment with respect to the origin suffer from
errors in both the model geometry and orientation amplified
by the symmetry elements; in addition, model vectors with
very high weight are less likely than in the rotation
search.
The phases calculated from the coordinates of an
oriented model are a continuous function of the shift
vector
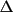 r. When the fragment is
moved through the unit cell keeping its orientation
fixed:
r. When the fragment is
moved through the unit cell keeping its orientation
fixed:
F
 =
F
=
F
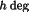 .
exp 2 π
h
.
exp 2 π
h
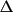 r
r
since all atomic displacements
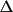 r are the same. So the
scattering contributions from the atoms of the search model
have to be summed only once for each orientation and
reflection to yield a structure factor
F
r are the same. So the
scattering contributions from the atoms of the search model
have to be summed only once for each orientation and
reflection to yield a structure factor
F
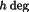 for the starting position; subsequently, the
structure factor
F
for the starting position; subsequently, the
structure factor
F
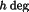 for any position is readily obtained by
multiplication with a simple phase factor. For the true
structure, the individual phases of the strongest
reflections are linked by various statistical phase
relations; amongst these, the three-phase structure
invariants have proved to be especially useful. The search
fragment is usually incomplete and may also be not very
accurate. Nevertheless, if its scattering power is
significant, the triple-phase relations should hold at
least approximately for the correct solution, in the sense
that the distribution of the phase sums is far from being
random.
for any position is readily obtained by
multiplication with a simple phase factor. For the true
structure, the individual phases of the strongest
reflections are linked by various statistical phase
relations; amongst these, the three-phase structure
invariants have proved to be especially useful. The search
fragment is usually incomplete and may also be not very
accurate. Nevertheless, if its scattering power is
significant, the triple-phase relations should hold at
least approximately for the correct solution, in the sense
that the distribution of the phase sums is far from being
random.
These considerations led us to the development of a
novel strategy for a Patterson translation search, which
exploits in an integrated fashion the information contained
in the sharpened Patterson function, the three-phase
structure invariants and allowed intermolecular distances.
In short, we have chosen the optimization of a weighted sum
of cosine invariants as our refinement procedure, with the
Patterson correlation and R indices as additional figures
of merit, and the minimum intermolecular distance as a
possible rejection criterion. This method is
computationally efficient, especially for larger
structures, because the refinement is based on phase
relations derived from a relatively small number of large E
magnitudes (say, >1.8). Only when an acceptable solution
has been found by this 'direct search' is it necessary to
calculate the time-consuming Patterson correlation.
Since, in order to save computing time, relatively
few phase relations are employed for the refinement, they
have to be selected carefully. Normally only the 40-60 most
probable and translation-sensitive three-phase structure
invariants are used for a translation search. It is
advisible to apply a
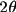 limit to the E
values before searching for phase relations, since
high-order reflections may be influenced considerably by
errors in the model. However, if the cut-off is too severe,
the accuracy of the phase-refinement procedure suffers. It
seems that a nominal resolution of about 1 Å is the best
compromise (
limit to the E
values before searching for phase relations, since
high-order reflections may be influenced considerably by
errors in the model. However, if the cut-off is too severe,
the accuracy of the phase-refinement procedure suffers. It
seems that a nominal resolution of about 1 Å is the best
compromise (
smax
0.5
in
GENEV
).
Then random positions are generated for the rotated
search fragment(s); it is our experience that about one
translation try per cubic Ångstrom is sufficient in
order to have a good chance of locating one search model
correctly (see
ntry
). Since the number of tries rises as a high
power of the number of independent fragments, it is
unreasonable to search for more than two fragments
simultaneously. However, any number of fixed fragments
(obtained from a previous search or a heavy-atom Patterson
interpretation, for example) may be added and, in fact, are
quite valuable provided their size or scattering power is
large enough.
Taking the limited range of the subsequent refinement
into account, only those random positions that are fairly
close to physically reasonable solutions are worth
refining; thus all positions that give rise to short
inter-molecular distances (say d <
p
Å) are immediately rejected (see
vmin
). The refinement procedure consists of two
cycles during which the translation parameters are refined
by optimizing
t3sum, which measures the triple-phase
consistency.
t3sum =
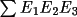 cos (
cos (
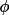
 +
+
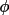
 +
+
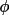
 )
)
t3sum is expected to be large and
positive for the correct solution. At the end of the second
cycle, only positions with
t3sum >
f
(see
tprt
) are regarded as possible solutions.
For solutions that have survived these tests, the
Tfom value is calculated identically as
for
Rfom but now for the inter-molecular
vectors. A small number of best solutions (according to
both
t3sum and
Tfom ) are stored provided that they
pass various tests for possible equivalence (allowed origin
shift or lattice translation). Although the true position
of the search fragment is usually recognizable at this
stage, R indices
Re1 and
Re2 based on E magnitudes have proved
very useful in distinguishing further between correct and
false solutions.
Finally, the solutions are sorted according to a
combined figure of merit:
Cfom = (
Rfom.
Tfom.
t3sum
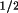 ) / ( 10 .
Re1.
Re2 )
) / ( 10 .
Re1.
Re2 )
For all solutions printed, a Patterson sum function
is calculated as a measure of fit/misfit for each
individual atom, taking all vectors (intra- and
inter-molecular) into account, this enables identification
of possible wrong atoms and thus model correction.
The procedure described differs from other Patterson
translation functions in that the oriented model is placed
with respect to all symmetry elements of the space group
simultaneously. Tests with known structures have indicated
that this routine is able to locate very large fragments
(of more than 300 atoms), in which case the distance tests
sometimes preclude the majority of trial positions, as well
as single atoms even when the latter are not very heavy
(e.g. phosphorus or sulphur in large organic structures).
Above all, the variety of different criteria employed to
judge solutions should make this combination of Patterson
and direct methods a powerful structure-solving strategy,
if chemical information is available. One would expect that
a position that is in agreement simultaneously with packing
criteria (dmin), the Patterson function (
Tfom ), triple-phase relations (
t3sum ) and E values (
Re ) is probably correct, and our
experience shows that this is indeed the case.
-
Reads symmetry & atom data from the input
archive bdf
-
Writes new atom sites to the output archive
bdf
-
Reads Patterson map from
mapfile
-
Reads E's and triplets from
invfile
-
Writes new atom sites to file
pch
This is the
lac1 test deck. It is the
standard test for PATSEE. Use the
lac1.dat
listing as a guide for other applications of
PATSEE.