XTINCT
: Extinction from equivalent reflections
Authors: Nick Spadaccini and
Douglas du Boulay
Contact: Syd Hall,
Crystallography Centre, University of Western Australia,
Nedlands 6907, Australia
This program calculates the isotropic Zachariasen
extinction coefficient r* by correlating the intensity
differences of symmetry equivalent reflections with the
diffraction path lengths through a nonspherical crystal.
The method is optimal for complete spheres of intensity
data, collected from crystals of higher
symmetry.
The greater accuracy required for high precision
density studies has led to the development of XTINCT. These
studies require a particularly careful treatment of the
correction factors for absorption and extinction, both of
which depend on the size and shape of the crystal.
Extinction coefficients determined from structure factor
least squares processes (such as
CRYLSQ
) are approximate because of correlation with other
intensity dependent errors.
XTINCT determines the isotropic extinction correction
factor from the measured intensity variations of
symmetrically equivalent reflections. This application
relies on a non-spherical crystal in which the path lengths
of symmetrically equivalent reflections are different. The
precision of the method depends on several factors: the
measured precision of the intensity data, the crystal shape
(non-spherical but well-defined faces so that accurate path
lengths can be calculated), the space group symmetry (the
higher the better) and the extent of the data measured (a
full sphere is highly desirable).
The correction for secondary (Type I) extinction is
based on the theory of Zachariasen (1967) and the
application procedure of Larson (1970). The corrected
measured structure factor is
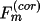 .
.

where
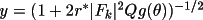
and
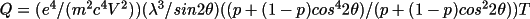
The function
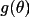 adapts the
formalism to several special cases of extinction. This is
necessary to ensure that the parameter r* is independent of
scattering angle.
adapts the
formalism to several special cases of extinction. This is
necessary to ensure that the parameter r* is independent of
scattering angle.
case 1 - Type II, primary
extinction
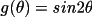
case 2 - Type I, secondary
extinction
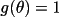
Parameter p specifies the fraction of total intensity
incident on the crystal specimen, that is polarised
perpendicularly to the diffraction plane of that specimen.
In the instance of neutron diffraction Q reduces simply
to
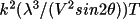 ,
,
where the neutron scattering length
 .
.
The secondary extinction coefficient r* is determined
by minimising the statistical variation of the intensities
for symmetry equivalent reflections. The minimum variance
is found when the first derivative of the variance
quadratic is zero. The derivative is taken with respect to
the extinction parameter r*, which in the isotopic case is
a scalar variable. In practice the quadratic is
approximated by a Taylor expansion about r* truncated at
the second order. The zero point of the first-order
differential equation is found analytically using an
iterative method which terminates when the shift in r* at
each iteration becomes less than 0.0001 of σ(r*).
The weighting of each set of equivalents is given by
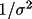 so that the stronger
reflection intensities dominate the refinement. In
accordance with the theory, the stronger reflections more
accurately reflect the effect of extinction.
so that the stronger
reflection intensities dominate the refinement. In
accordance with the theory, the stronger reflections more
accurately reflect the effect of extinction.
XTINCT works best when applied to a full sphere of
measured intensities. This provides as many equivalent
reflections as possible. The strong dependence of the
refinement on path length variations between equivalents
restricts its application to non-spherical crystals. The
procedure is applied after absorption corrections and
applied to clustered F squared data.Here are the
calculation steps needed for the application of XTINCT.
This is when extinction is applied to |F|
 data. See example 4 for a typical input file which
parallels these steps.
data. See example 4 for a typical input file which
parallels these steps.
-
A full sphere of intensity data should be
collected from a single non-spherical crystal and
processed with the
STARTX
and
DIFDAT
steps.
-
The intensity data is then processed using
SORTRF aver 2 to
calculate the merge R-factor
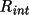 .
The output of this run is NOT
saved.
.
The output of this run is NOT
saved.
-
The intensity data from step 1 is then corrected
for absorption using the program
ABSORB
. The
tbar
option must be set so that the mean
path lengths of the individual reflections are stored
on the bdf. An analytical absorption calculation is
recommended for the most precise path lengths.
-
The output bdf from
ABSORBis processed with
SORTRF aver 2 to
again calculate the merge R-factor
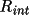 .
The output of this run is NOT
saved. This is to check the effect of the
absorption corrections on the equivalent data.
.
The output of this run is NOT
saved. This is to check the effect of the
absorption corrections on the equivalent data.
-
The output bdf from
ABSORBis processed with
SORTRF clus to
cluster equivalent reflections into sequential
groups.
sepfrl is required to
group Friedels separately, if a non-centrosymmetric
structure. This output
is saved.
-
The clustered intensities from
SORTRF
are converted to
structure factors squared with
ADDREF nobay and
reduce
itof2.
-
Then use
GENEV enot to
determine the scale factor between observed and
calculated structure factors. This is essential to
place the extinction coefficient r* calculated in the
next step on an absolute scale.
-
Apply the XTINCT program (a description of the
input options is below).
-
Apply
ADDREF nobay and
reduce f2toi to
convert the F squared to I.
-
Apply
SORTRF aver 2 for
the fourth time to yield the final R-factor
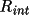 . This provides
the final measure of the effect of correcting for
extinction and absorption.
. This provides
the final measure of the effect of correcting for
extinction and absorption.
-
Finally apply
ADDREF nobay and
reduce itof to
reduce the intensities to F.
In the default mode XTINCT calculates, refines and
applies the extinction coefficient r* to the
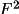 data. This data is
output to the bdf along with the value of r* (on the
absolute scale supplied from the prior
data. This data is
output to the bdf along with the value of r* (on the
absolute scale supplied from the prior
GENEV
run). 25 reflections will be printed.
Options on the
XTINCT line and on the
limits line provide for
various controls on this calculation. The coefficient r*
may be determined within specific regions of the data using
the
limits control line
(though the resulting r* is then applied to all data). The
value of r* may also be determined separately for each set
of equivalents by entering the
sall
option (the resulting values are output to
the
PCHfile). A
value of r* may be input and applied using the
appx
option. Because sets of equivalent
reflections with identical tbars can result in
singularities, or negative r*, these sets are automatically
skipped in the refinement. They may, however, be included
using the
incl
option. Similarly, large anomalous dispersion
difference between Friedel related reflections (for
non-centrosymmetric spacegroups) can effect the refinement
of r* and these will normally be treated separately, but
will be treated as symmetrically equivalent reflections if
the option
eqfr
is entered. The polarisation factor p, if
unavailable on the bdf and not included as an option on the
title line, takes the default value of unpolarised
radiation (0.5).
-
Reads reflection data from the input archive
bdf.
-
Outputs corrected (or uncorrected) data on the
output archive bdf.
-
Optionally outputs a
pchfile.
This is the standard run which refines and applies
the extinction coefficient dat to the
 data. 25 reflections
will be printed and the scaled r* value will be stored on
the output bdf.
data. 25 reflections
will be printed and the scaled r* value will be stored on
the output bdf.
The extinction r* will be refined on all sets of
equivalents for which the average
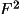 lies between 1000 and
100000. All reflections will be printed, and the Friedel
related intensities will be treated as equivalent
reflections.
lies between 1000 and
100000. All reflections will be printed, and the Friedel
related intensities will be treated as equivalent
reflections.
The unscaled extinction correction r* of 153 and a
sigma r* of 22 will be applied to the data. The first 40
reflections on the bdf will be printed.
-
Becker, P.J. Coppens, P. (1974)
Acta Cryst
A30, 129-147.
-
Olthof-Hazekamp, R. (1991)
Xtal3.4 Manual, CRYLSQ.
-
Larson, A.C. (1970) p292
Crystallographic Computing :
Munksgaard.
-
Maslen, E.N. Spadaccini, N. (1992)
Acta Cryst.
A49, 661-667.
-
Spadaccini, N. (1989)
Proceedings of CRYSTAL XVI,
Lorne SCA Meeting.
-
Zachariasen, W. H. (1967)
Acta Cryst
23, 558-564.