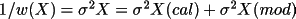|
| A = 1 : from LSW1(n901) to LSWT(n900) |
| B = 2 : from LSW2(n902) to LSWT(n900) |
| C = 3 : from LSW3(n903) to LSWT(n900) |
Scheme 1:
W = 1 / (A + B

 X + C/(oldweight) + D*X(rel) + E*X(rel)
X + C/(oldweight) + D*X(rel) + E*X(rel)
 + G*X(rel)
+ G*X(rel)
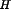 + I*sin
+ I*sin
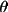 )
)
Scheme 2:
W = 1 / (A + B*X(rel) + C*X(rel)
 /oldweight + D*X(rel)
/oldweight + D*X(rel)
 + E*sin
+ E*sin
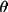 )
)
Scheme 3:
W = X * Y If A*X(rel) is greater than |X(cal)|
then weight is 0.000000001. Let B = sin
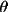 limit, then if sin
limit, then if sin
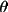 is greater than B,
X = 1, else X = sin
is greater than B,
X = 1, else X = sin
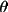 /B
B should not be zero. Let C = X(rel)
limit, then if X(rel) is less than C, Y = 1, else Y =
C/X(rel).
/B
B should not be zero. Let C = X(rel)
limit, then if X(rel) is less than C, Y = 1, else Y =
C/X(rel).
Scheme 4:
If X(rel) is less than or equal to A, then W =
(X(rel)/A)
 , else W = (A/X(rel))
, else W = (A/X(rel))
 . Reflections with X(rel) = A are given maximum
weight.
. Reflections with X(rel) = A are given maximum
weight.
Scheme 5:
If X(rel) is less than or equal to A, then W =
1, else W = (A/X(rel))
 . Small reflections are given constant weight. In
Hughes' original treatment, A = 4 X(min).
. Small reflections are given constant weight. In
Hughes' original treatment, A = 4 X(min).
Scheme 6:
W = 1 /(1 + ((X(rel) - B)/A)
 ) Reflections with X(rel) = B are given maximum
weight, but if A is very large , the weights are
constant.
) Reflections with X(rel) = B are given maximum
weight, but if A is very large , the weights are
constant.
Scheme 7:
W = 1 /( A + X(rel) + B*X(rel)
 + C*X(rel)
+ C*X(rel)
 ) Cruickshank suggests that A = 2 X(min), B = 2 /
X(max), and C = 0 are useful. A larger value of C, say C =
5 / X(max)
) Cruickshank suggests that A = 2 X(min), B = 2 /
X(max), and C = 0 are useful. A larger value of C, say C =
5 / X(max)
 , may help down-weight large X(rel) subject to
extinction. These values may prove useful in schemes 1 and
2.
, may help down-weight large X(rel) subject to
extinction. These values may prove useful in schemes 1 and
2.
Scheme 8:
W = A / max(
 X(rel), (B*X(rel)
+ C), (D*G + E) )where G is X(rel)(max). For a complete
description of this (Univ. of Washington) scheme, see the
general section for the program DATRDN of the XRAY76
system.
X(rel), (B*X(rel)
+ C), (D*G + E) )where G is X(rel)(max). For a complete
description of this (Univ. of Washington) scheme, see the
general section for the program DATRDN of the XRAY76
system.
Scheme 9: W = A This weighting scheme produces constant weights
If the variances of the structure factor amplitudes
are correctly estimated, their average value should
correspond to
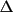
 X. (The variance will be assumed to represent
error in both the experiment and the model; i.e. in
|X(rel)| and |X(cal)|.) The process of least squares allows
some adjustment of the model to errors in the experiment,
so that
X. (The variance will be assumed to represent
error in both the experiment and the model; i.e. in
|X(rel)| and |X(cal)|.) The process of least squares allows
some adjustment of the model to errors in the experiment,
so that
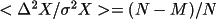
rather than unity. N is the number of reflections
used for least-squares refinement and M is the number of
least-squares variables. <A> is the average value of
A. The quantity (N-M)/N will be referred to in what follows
as the "freedom factor". The calculated variance,

 X(cal), is the variance obtained from a knowledge
of the experimental conditions and is usually based
entirely on counting statistics. A quantity
X(cal), is the variance obtained from a knowledge
of the experimental conditions and is usually based
entirely on counting statistics. A quantity
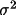 X(mod), the modified
variance, may be added to
X(mod), the modified
variance, may be added to
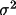 X(cal) to give an
improved value of
X(cal) to give an
improved value of
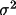 X or 1/w(X). The
correction,
X or 1/w(X). The
correction,
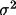 X(mod), commonly
called the "ignorance factor", may be entered by the user
as some function such as
X(mod), commonly
called the "ignorance factor", may be entered by the user
as some function such as
(see Scheme 1, normal weighting schemes) or it may be
estimated automatically. An approximate expression for
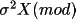 is
is
where VC is a correction term including variance (VAR) and covariance (COV) terms.
This term results from replacing
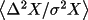 by
by
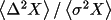 ,
and the user may choose to not use it.
Also, the "freedom factor" may be replaced by unity. The
independent variables are normalized by dividing by
,
and the user may choose to not use it.
Also, the "freedom factor" may be replaced by unity. The
independent variables are normalized by dividing by
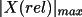 and
and
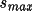 .
The new independent variables are:
.
The new independent variables are:
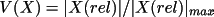
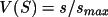
The correction,
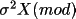 , is estimated
by least-squares fitting of the following expression to
equation ???
, is estimated
by least-squares fitting of the following expression to
equation ???
If p=0, a constant term is determined.
If p=1, the coefficients in the expression of the form
A(0,0) + A(1,0)*V(F) + A(0,1)*V(S)
are determined; etc.
The coefficients A(p,q) can then be used to calculate
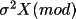 for an individual reflection. The weight
for a reflection is then calculated as:
for an individual reflection. The weight
for a reflection is then calculated as:
The structure is refined by normal least squares
using the modified weights and new values of
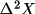 are created. If the
individual reflection option is chosen, the variance and
covariance correction is not used or calculated. The
process is iterated until the coefficients do not change.
The change in the standard deviations of least-squares
variables on the first iteration will probably be between 0
and 40% of their initial value with non-modified weights.
The improvement on the second iteration will typically be
10% of the improvement of the previous one. A third
iteration would seldom seem justified. The quantity
are created. If the
individual reflection option is chosen, the variance and
covariance correction is not used or calculated. The
process is iterated until the coefficients do not change.
The change in the standard deviations of least-squares
variables on the first iteration will probably be between 0
and 40% of their initial value with non-modified weights.
The improvement on the second iteration will typically be
10% of the improvement of the previous one. A third
iteration would seldom seem justified. The quantity
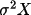 is required for
calculating the variance and covariance correction (VC),
but is not well known until after first iteration.
Therefore
is required for
calculating the variance and covariance correction (VC),
but is not well known until after first iteration.
Therefore
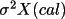 must be used
instead of
must be used
instead of
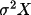 in the first
iteration, if the VC correction is applied.
in the first
iteration, if the VC correction is applied.
In the REGWT calculation, the value of
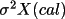 in
(4.85) above is
obtained from IDN 1900 in logical record
in
(4.85) above is
obtained from IDN 1900 in logical record
lrrefl:
on the bdf. If IDN 1900 is empty, the value of
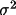 X(cal) is then
obtained from IDN 130n (n=1, 3 or 5 for I,
X(cal) is then
obtained from IDN 130n (n=1, 3 or 5 for I,
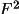 or F, respectively).
After the modified weight w(X) is calculated, its value
will be stored in IDN 1900, replacing the old value of
or F, respectively).
After the modified weight w(X) is calculated, its value
will be stored in IDN 1900, replacing the old value of
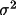 X(cal).
X(cal).
The square root of the number of reflections in a grid point is used to weight the grid points when fitting equation (4.84) to equation ???. Not surprisingly, grid points with high V(X) and high V(S) may be empty and others may have few reflections. The option also exits to not average but treat every reflection as a separate grid point. Since averaging to form grid points involves first order differences, the influence of reflections whose contribution to the average in equation ??? deviate far from the mean will be enhanced if individual reflections are used to find the A(p,q). If the individual reflection option is chosen, the variance and covariance correction is not used or calculated.
-
Reads reflection data from the input archive bdf
-
Optionally writes reflection data to the output archive bdf
REGWT lst wta maxhkl 12 12 12 0.0 0.824 fgrid 2.3 4.3 7.6 12.4 fgrid 13.4 17.5 20.5 25.5 30.5 35.5 fgrid 45.0 55.5 65. 80. 100. 99999. sgrid .1 .15 .2 .25 .3 .35 .4 .45 .5 .55 .6 .65 sgrid .7 .75 .80 .85
In this example, the weight-analysis process is called to analyze the weights which have been assigned for each reflection. The analysis maps are specified as 16x16 by the fgrid and sgrid lines. The program does not update the archive bdf. The reflection data will be printed.
REGWT nolist wfc 10.0 rel cnt 99.0 regina pow 2 ind fac 1. avc archiv 1902 -1903 fgrid 3.0 4.0 5.0 6.0 7.0 8.0 fgrid 9.50 12.0 17.0 21.0 27.0 30.0 50.0 fgrid 70.0 999.0 sgrid 0.150 0.200 0.250 0.300 0.350 0.400 0.450 sgrid 0.500 0.515 0.530 0.550 1.000
The weight modification function with 2 as the highest power is specified. The estimation of the weights is based on the individual reflection mode. The variance and covariance correction is applied and the least-squares freedom factor is 1. The weight in location 1903 will be deleted from the binary data file and the old weight will be stored in the weight location 1902. Only the observed reflections are used excluding the reflections for which the value of ?(F) is greater then 99.0. The output analysis map (15x12) will be scaled by the factor 10.
REGWT nor normal 0 b 2 archiv -1903
A normal weighting scheme is indicated in the REGWT line. The scheme number is specified as 0, which transfers the weight saved at location 1902 to location 1900 where it will be used for weighted least-squares refinement. The old weights at location 1903, if they exist, will be erased from the bdf.
References
-
Wang, Hong and Robertson, B.E. 1985. Structure and Statistics in Crystallography.Ed. A.J.C. Wilson. Adenine Press: New York.
-
Stewart, J.M., Machin, P.A., Dickinson, C.W., Ammon, H.L., Heck, H. and Flack, H.D. 1976. The XRAY76 SYSTEM. Tech. Report. TR446, Computer Science Center, University of Maryland.
-
Prince, E. 1982. Mathematical Techniques in Crystallography and Materials Science. Springer-Verlag: New York.
-
Johnston, R.L. 1982. Numerical Methods -- A software approach. John Wiley: New York.
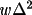
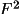
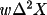
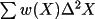
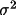

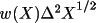
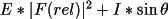
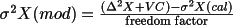
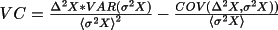
![\(
\Mean{\sigma ^{2}X(mod)} = \sum_{p}(\sum_{q}{[A(p-q,q)]
[V(X)^{p-q}] [V(S)^{q}]})
\)](equations/4.55.3-eq-84.gif)