The Fourier map entered from the mapbdf must contain enough points so that every point in the output plane is represented. The simplest way to ensure this is to input at least the map of the asymmetric unit of the cell. Any map type may be used (e.g. Patterson, E map, difference map). The computed map may be printed or output to the bdf sla, with the same structure as map, for use with programs such as CONTRS . The optional output is printed in base-10 integer format ( normal ) with the map density scale, upper and lower print suppression limits and map format under user control. The output options are invoked on the SLANT line.

Note that all input map points are stored in the QX array. Depending on the size of the unit cell, and on the resolution desired, this program requires a very large memory allocation.

There are two coordinate systems involved in the program. The first is the crystallographic coordinate system defined by the crystal symmetry. The other may be thought of as the calculated coordinate system and is determined relative to the general slant plane. The calculated coordinate system is orthogonal with two vectors in the general plane and the third normal to the plane. All information concerning the definition of the general plane is in terms of crystallographic coordinates and the layout of the computed map is specified in terms of calculated grid coordinates. Since the calculated coordinate vectors have no absolute length, the grid interval can be explicitly specified in angstroms per division. If not specified the program takes the average of the input map resolution as the output grid interval.

Three non-collinear points which define the required plane are specified on the defpln line in either grid or fractional crystallographic coordinates. The two in plane vectors defined by these three points are used to generate an orthogonal coordinate system which characteristically defines its origin to be the first supplied point, the vector between the first and second points is defined to be a(calc), the normal to the plane is b(calc) and the vector product of these is c(calc). The grid interval widths in angstroms for each direction in the calculated coordinate system may be defined on the mapres line.

The layout line specifies the desired orientation of the maps relative to the calculated coordinate system. The three vectors a(calc), b(calc) and c(calc) must be specified as either the page to page, down page or across page directions. The layout line allows entry of the number of grid points, the origin, and the stepping interval for each of the three directions in the map. With the absence of a layout line the program will produce an output of the plane containing the three points supplied on the defpln line. The number of grid points in the a(calc) and c(calc) directions is determined so that all three points just fit within the map.

Linear interpolation from the input Fourier map to produce the slant plane map leads to the shortest calculation times. Each map point on the required plane is expressed in terms of the original crystallographic grid coordinates. The program is written to select 8 of the supplied map points closest to this point and to interpolate linearly. Assume that the required map point is at (x+pX,y+qY,z+rZ) in crystallographic grid coordinates, where X, Y and Z are the grid intervals. The grid point less than x+pX is designated as 1 and that greater than x+pX is designated as 2. The same definition holds for y+qY and z+rZ. The trivariate interpolation formula with the origin at 111 is as follows:

v(x,1) = 1 - p

v(x,2) = p

and similarly for

v(y,j) and v(z,k) where j, k = 1, 2

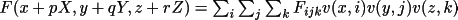
A slower, but more accurate, method of interpolation uses the cubic algorithm. It may be found useful or necessary when the input Fourier grid is at low resolution. The interpolation algorithm to be used is specified on the SLANT line. The cubic method is estimated to be more accurate by a factor of ten than the linear method. It is, however, a factor of five slower. The use of either method is much faster than the calculation of an exact general plane Fourier transform. It should be noted that a cubic interpolation using a coarser grid resolution is comparable to a linear interpolation at roughly twice the resolution and thus requires much less memory to store the input map. The cubic algorithm uses the nearest 64 points and uses the following formula. The same notation is used again, but with the origin at 222:

v(x,1) = - 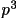/6 + 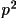/2 - p/3

v(x,2) = 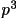/2 - - p/2 + 1

v(x,3) = - 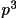/2 + /2 + p v(x,4) = 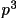/6 - p/6

and similarly for v(y,j) and v(z,k) j, k = 1, 2, 3, 4

By the use of site or siteg lines the user may obtain positional parameters relative to the slant plane in terms of calculated grid coordinates.

SLANT file nprint cubic       
defpln frac 0 0 0 .56 .24 .31 .74 .86 .21       
mapres .15 .15 .15       
layout across layer down 21 1 21 -10 0 -10 1 1 1

In this example the map is mot printed but is output to bdf SLA. Cubic interpolation is used. The lines defpln, mapres and layout refer to the general plane coordinate axes a-calc, b-calc, c-calc. These axes are defined by the points, in fractional coordinates, given on the defpln line. The layer direction is b-calc, with c-calc down the page. Only one layer is to be calculated with 21x21 points passing through the origin, starting at -10 in both directions. Given the resolution of 0.15 Å/div., the output map is 3.x3.Å with origin at the centre and defined as (0,0,0)

SLANT nfile print linear       
defpln grid 10 20 30 17.5 1.5 13.3 18.5 54.6 12.3

The output map is printed only. Linear interpolation is used. The slant plane is defined by the points on defpln. These refer to the original grid coordinates used in FOURR . The average resolution used in FOURR will be applied. The ouput plane will be large enough to contain the three points that define the plane.