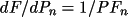|
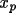 is not
applicable is not
applicable |
for ZACH |
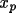 = 0 = 0 |
for TYP1 |
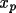 = =
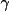
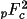
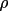
 |
for TYP2 and GEN |
The secondary (type I) extinction varaiables are:
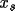 = r* = r*
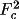
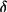 |
for ZACH |
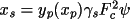
|
where
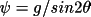
|
for TYP1 |
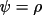
|
for TYP2 |
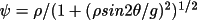
|
for GEN with a Gaussian distribution |
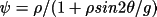
|
for GEN with a Lorentzian distribution |
These expressions indicate the strong dependence of
the extinction correction on
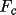 . For given g or
. For given g or
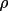 , different values
of y can be obtained depending on the structure factor
model. This is a consequence of the Zachariasen or Becker
and Coppens formalism for the
posteriori correction of intensities
for extinction.
, different values
of y can be obtained depending on the structure factor
model. This is a consequence of the Zachariasen or Becker
and Coppens formalism for the
posteriori correction of intensities
for extinction.
For the Zachariasen correction, r* is equal to the
final value of EXT printed by CRYLSQ
multiplied by
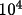 . That
is, if EXT=.2 then r*= 2000. If one assumes that the
extinction is Type I then r* = g. If one assumes a Type
II extinction then r* =
. That
is, if EXT=.2 then r*= 2000. If one assumes that the
extinction is Type I then r* = g. If one assumes a Type
II extinction then r* =
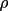 .
.
The values of g and
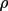 obtained are
dimensionless and relate to the physical properties of
the crystal in the following manner,
obtained are
dimensionless and relate to the physical properties of
the crystal in the following manner,
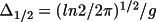 radians radians |
(
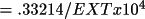 ) for the
Gaussian distribution ) for the
Gaussian distribution |
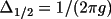 radians radians |
(
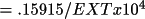 ) for the
Lorentzian distribution, where the half width ) for the
Lorentzian distribution, where the half width
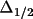 of the
distribution indicates the mosaic spread of the
distribution indicates the mosaic spread |
| r = ρλ | (
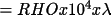 ) where r is thesize of the
mosaic blocks and λ the
wavelength ) where r is thesize of the
mosaic blocks and λ the
wavelength |
The absolute-structure (twin) parameter xabs may be used to define the absolute configuration or polarity of untwinned crystals (Flack, 1983). The crystal is described as an inversion twin. 1- x and x are the fractions of the structure and its inverse in the macroscopic sample. The structure factor equation is given by
|F(h,k,l,
xabs )|
 = (1-
x ) |F(h,k,l)|
= (1-
x ) |F(h,k,l)|
 +
x |F(-h,-k,-l)|
+
x |F(-h,-k,-l)|

xabs converges in 2 to 4
cycles, depending on the anomalous dispersion
contribution, to values between 0. and 1., within 3
e.s.d.'s. Friedel pair measurements must be present in
the bdf for all or part of the reflections. Note that the
option needs to be used in SORTRF to pack
pairs into a single packet.pakfrl
All positional parameters for selected atoms are refined unless a noref condition is present to direct that a parameter be held invariant.
The program can be used to refine the values of
overall, isotropic, anisotropic or mixed thermal
displacement parameters. In the mixed mode these
parameters are set in accordance with the specification
stored in the bdf. For one or more atom types the mode
can be changed by the use of a
dptype line. In the
program, use is made of
u or
uij. On the printed
output, U values (multiplied by 100) are displayed. After
correction, the displacement parameters are tested to be
sure of their physical significance. If an isotropic
thermal displacement parameter is negative or an
anisotropic displacement tensor is not positive definite,
a warning is printed. When a displacement parameter is
found to be non-positive definite one of three options
can be specified in the
CRYLSQ line -- continue
with calculated values (
), reset displacement to positive definite
and continue (
tw
), or stop (
tr
).tt
When one or more atoms has an overall thermal displacement parameter and the use of a full matrix is specified, derivatives are calculated with the formulae that is used for the uov, but summation is over only those atoms with uov. When other block types are used, the summation for UOV is over all atoms.
The term population parameter is used to describe
the occupancy of an atom site. It is independent of atom
multiplicity for the site. Population parameters are
applied in the calculation only when they are present in
logical record
lratom:
of the bdf. Their refinement flag is turned on
by the
code in the
CRYLSQ line.
noref lines can be used
to turn off refinement of indicated population
parameters.pp
The normal equations are solved by the method of Choleski. A is a positive definite, symmetric matrix. It is decomposed to an upper triangle U and a lower triangle L. Matrix L is the transpose of U, so only enough memory to hold half the matrix is required.
From the decomposed triangle U the shifts can be calculated easily.
The estimated standard deviations are derived by the following expression where n is the number of reflections and m is the number of variables:
For the calculation of standard deviations, the inverted matrix is required. It is obtained by inverting the triangular matrix. Because the inversion is a rather time consuming, the standard deviations are calculated only during the last cycle.
There are several options for blocking the matrix of normal equations, A.
-
All parameters may be refined in one block. This is referred to as full matrix and is specified by
fm -
The matrix may be blocked so that there is one block for the parameters of each atom. This is referred to as block diagonal and is specified by
bd -
The matrix may be blocked in such a way that each block contains the parameters for more than one atom. The option is specified by
bl -
The matrix may be divided into blocks containing any arbitrary parameters. This option is indicated by
bl
Parameters can be held invariant by two methods:
By commands from logical record
lrcons:
of the bdf. These commands are generated by
the program ADDATM and specify atoms in special position.
See the documentation on ADDATM for details.
By a noref line. The general form for the invariant parameter set is:
| (P1/P2)(R1/R2) or (P1,P2)(R1,R2) or any combination of these | |
| P1/P2 parameter symbols P1 to P2 inclusive (see lists below) | |
| P1,P2 parameters P1 and P2 only | |
| R1/R2 atom name's R1 to R2 inclusive | |
| R1,R2 atom name's R1 and R2 only |
If only an atom name or atom type is present, then all the parameters for that atom or atom type are held invariant. If only a parameter is specified, then that parameter is held invariant for all atoms. More than one invariant parameter set may be input on a noref line. In addition to the individual atom parameters the following general parameters may also be specified invariant:
|
scale factor(s) |
|
overall thermal displacement parameter |
|
extinction parameter(s) |
|
dispersion factors |
The individual atom parameters are: (See
the program
ADDATM
for definitions)
x y z u u11 u22 u33
u12 u13 u23 pop app neu
There exist atom types Y and U. In these cases, parameter symbols and atom types must be present.
noref y(c3) : y invariant for atom c3 noref (x,z)(c2,c5) : x and z invariant for atoms c2 and c5 noref (x/u11)(c1/c3) : x to u11 invariant from atom c1 to c3 noref u : u invariant for all atoms noref c5 : all parameters invariant for atom c5 noref u(h) c : u for h atoms and all c parameters invariant
Parameters may be constrained to be relative to other
parameters by: the space group symmetry requirements of an
atom sited at a special position, the requirements of
definition of the origin in polar space groups or use of
the
constr option as
specified by the user.
ADDATM
will detect atom parameters constrained by space
group symmetry or polar space group requirements and store
the information in logical record
lrcons:
of the bdf.
The general form of a constraint equation on the constr line is:
par(s)(atom(s)) = Q + fct(1)*par(1)(atom(1)) +...+ fct(n)*par(n)(atom(n))
where
| par(s) | = subject (dependent) parameter |
| atom(s) | = subject (dependent) atom name |
| Q | = constant term |
| par(1,2,..,n) | = reference (independent) parameter(s) |
| atom(1,2,..,n) | = reference (independent) atom name(s) |
| fct(j) | = multiplication factor for corresponding parameter par(j) |
Note that the subject parameter or atom must not precede the reference parameter or atom in the parameter or atom list. That is,
y(Cu1)=0.0+2.0*x(Cu1)
|
is correct |
x(Cu1)=0.0+0.5*y(Cu1)
|
is not correct |
x(Cu2)=0.5+1.0*x(Cu1)
|
is correct |
x(Cu1)=0.5+1.0*x(Cu2)
|
is not correct |
Two examples follow:
constr x(c1)=0.5+1.0*y(O2)-0.5*z(C3) constr pop(al1)=1.0-1.0*pop(Mg2)
Though the first example is unlikely it illustrates
the general form of a
constr line input. The
use of the
constr line restricts the
value of the x parameter of the atom
C1to be equal
to the y parameter of
O2minus half
of the z parameter of
C3plus a
constant term. The second example is common in mineral
structures where stoichiometric disorder occurs at atom
sites. The total population of the two atom types at the
site must sum to a population of one.
If the input parameters do not satisfy the above equation prior to refinement, they are modified to do so, except when the constant value Q is given as the letter Q. The applied shifts always satisfy the constraint equation.
In polar space groups the position of the origin in one or more directions is not fixed by symmetry elements. Coordinates in a polar direction can be considered as a special case of constraints. One polar coordinate depends on all others.(The factors are negative 1.) In the block diagonal approximation polarity does not have to be considered, because it will not lead to singularity of the matrices.
The contribution of the dependent parameters to the derivatives of the reference parameters is expressed in the chain rule where sum(i) is the sum over all parameters dependent on p(j), including the derivative of p(j) itself (Finger, 1969).
The standard deviation of the dependent parameter is calculated according to the approximate formula:
where COV(j,k) is the covariance of the jth and kth reference parameters.
The total number of parameters in a structure can be
reduced if some subset of the atoms can be considered as a
rigid group. Idealized coordinates for rigid groups can be
calculated and written to the bdf either by the program
RIGBOD
or by the program
BONDAT
. Another method of reducing the total number of
parameters is when a structure contains two or more
fragments consisting of "identical" points. These are
referred to as identical molecules. Using the identical
molecule, two or more groups of atoms in a crystal
structure can be forced to maintain the same intermolecular
structure during the refinement.
In both cases use is made of the Euler parameters: three coordinates of the centre of gravity and three angles that relate the principal axes of the group to the cell axes respectively, to the principal axes of the first identical molecule. For the Euler angles the Goldstein definition from classical mechanics is used. The calculation of the principal axes is accomplished by the diagonalization of the inertia tensor by the method of Jacobi.
For a non-degenerate inertia tensor three non-collinear atoms are needed in the rigid group. Groups positioned on a symmetry element lead to dependent or invariant Euler parameters. Information on fixed parameters must be given in the group line; dependency must be given in constr lines for the first atom(s) of the group(s).
Thermal displacement parameters and population parameters can be refined either for the individual atoms or for the groups (for group isotropic displacement parameters only). Dependencies of these parameters for different groups can be maintained by the use of constr lines. When there is only one displacement parameter or one population parameter for a group, one constr line will suffice (for the first atoms of the groups).
The use of stereochemical data as individual observational equations was first proposed by Waser (1963). In CRYLSQ these eqquations are referred to as restraints. The atom model is restricted to a realistic range of geometries. The weights are inversely related to the standard deviation of the distribution of possible values. The extra term to be minimized by the least squares process is
where
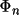 is either the bond distance, bond angle, or
dihedral angle; and
is either the bond distance, bond angle, or
dihedral angle; and
The process of refinement of a crystal structure utilizing a nonlinear least-squares procedure requires some attention to be given to the weight assigned to each experimental observation. In the XTAL system, the quantity stored in the binary data file is the square root of the reflection weight (this convention has arisen because it saves many thousands of multiplication operations during the building of the matrix and vector of the normal equations). The practice follows that established in ORXLS (Busing and Levy, 1959) and is common to many least squares programs.
The derivation of the values of the weights is a
matter of considerable controversy in the crystallographic
literature. For this reason, a number of methods of dealing
with the problem of establishing values suitable to the
user are provided. The weights to be applied may be
specified in three different ways: a weight of 1.0 for all
observations (
), a weight of 1/
wu

 F (
F (
), or the weights supplied in the bdf (
ws
).ww
In all block modes a partial shift factor of 0.8 is
automatically applied. The factor may be changed by using
the code
in the
CRYLSQ line. The factor
which is used will depend on the correlation between atoms
in different blocks. When correlations are high, a small
shift factor should be applied to damp the shifts.fu q
Poorly measured data points can be treated in a
number of ways. A broad category, referred to as less-thans
(rcode=2) may be suppressed from the data set by the
option in the
CRYLSQ line where the
threshold of observability is defined in terms of multiples
of
tl q
 (F,
(F,
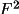 , or I).
, or I).
In general, less-thans are not contributed to the
least-squares matrix. This can be overridden by the
option on the
CRYLSQ line which forces
all less-thans with a
ml
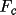 greater than
greater than
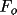 to contribute to the
matrix. Only those reflections considered to be more
accurately measured (where the weight*
to contribute to the
matrix. Only those reflections considered to be more
accurately measured (where the weight*
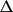 (F) is less than
some user defined quantity
(F) is less than
some user defined quantity
) can contribute to the matrix by the
q
option in the
CRYLSQ line. When this
reclassification is specified, it is only applied during
the current calculation. It will not be written to the
bdf.mr q
Scattering factors are entered from the bdf. If
interpolated scattering factors are present on the
reflection data record
lrrefl:
(as inserted by
ADDREF
), these will be used. Otherwise, scattering factors
are extracted from the form factor tables on
lrscat:
.
![[Warning]](../graphics/warning.png) |
Warning |
|---|---|
|
The scattering factors from the form factor tables are considered sufficiently reliable for routine analyses with R-factors above 0.03. For more accurate analyses the interpolated form factors must be used. |
The CRYLSQ program is general with respect to symmetry. The symmetry operations stored in the bdf are used to generate all the symmetrically equivalent points for the asymmetric set of reflections and atoms supplied. It is important to note that there must be no systematically absent reflections coded as observed reflections (rcode=1 or 2) included in the data supplied.
The number of unique atoms which is used for the
calculations may be limited. The structure factor
calculation and refinement procedure can be carried out
with a selected set of atoms (use the
select line). Fixed
contributions to the structure factors for the remaining
atoms must have been calculated in a former structure
factor calculation with
FC
or
CRYLSQ. By using
in the
CRYLSQ line the fixed
contributions ar applied as partial contributions too the
structure factor sums and they are stored in
ep
lrrefl:
(IDN 1810 etc.). In subsequent runs, with the
same selected atom set, the same fixed contributions may
again be applied (
in the
CRYSLQ line). In this way
it is possible to carry out blocks of refinements of
various parts of the structure to achieve overall
refinement of the complete structure.ap
During the initial steps of refinement it is not always necessary to use all reflections. The number of reflections can be limited by:
-
Defining a sin
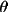 /
/
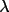 range in a
maxhkl line.
range in a
maxhkl line. -
Assignation of maximum h, k and l values in a maxhkl line.
-
Skipping of reflections with the
sk n
The following formulae give the equations used in the calculation of the derivatives of F(cal) required in the building of the least-squares matrices.
The structure factor equation (4.7) can be written as:
where
and
The factors A/F and B/F are introduced to relate the phases of the partial derivatives with the phase of F. The formulae for the derivatives are:
where n' is the atoms with overall thermal displacement parameter. When uov is used for the correlation correction, the summation is over all atoms.
-
Reads atom and reflection data the input archive bdf
-
Writes refined atom and reflection data the output bdf
-
Optionally writes correlation matrix to file
cmx -
Optionally outputs atom lines to the line file
PCH
CRYLSQ
The input above causes all the defaults to be taken
by CRYLSQ. All positional and thermal parameters of all
atoms on the bdf will be refined in a single cycle of block
diagonal refinement based on F(rel). The thermal
displacement parameter type used in the calculation for
each atom will be read from logical record
lratom:
of the bdf.
CRYLSQ f2 cy 3 is bl block N1 N2
The compound used in this example is 4,4'-dinitrodiphenyl.
O1 C12--C1 C23--C22 O3
\ / \ / \ /
N1-C11 C14--C24 C21-N2
/ \ / \ / \
O2 C16--C15 C25--C26 O4
The bdf for this example has been formed so that the
first atom in
lratom:
is N1. It is followed by O1, O2 and carbon atoms
C11 through C16. After these atoms comes N2 and then the
remaining atoms. The
block line requests that
the matrix be blocked in two pieces, each block containing
the atoms of one of the rings. Such a blocking scheme can
be useful at early stages of refinement or when there is
insufficient storage to hold the entire matrix. The
information on the
CRYLSQ line specifies
three cycles of refinement on
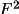 with isotropic thermal
displacement parameters for all atoms.
with isotropic thermal
displacement parameters for all atoms.
CRYLSQ is group atomgr N1/C16 group atomgr N2/C26 constr u(N2)=0.0+1.0*u(N1)
Both parts of the molecule are refined as rigid groups. There is only one isotropic thermal displacement parameter for all 18 atoms.
ADDREF dset 1 extf reduce f2tof rlp2 neut hklin hkl f2rl sgf2 hkl 0 0 2 5.227 1.303 hkl 0 0 4 19.679 2.195
............................................reflection data omitted for brevity
CRYLSQ asn nu f2 ws rx cy 3 fm scale 0.2295 1 extinc *4 .11726 noref C1/H10 CRYLSQ asn nu f2 ws l1 cy 2 fm rx
This example shows a run in which a set
of neutron data with a Zachariasen's secondary extinction
correction is refined. The
ADDREF
run shows the setting up of the reflection
extinction factors. Two runs of CRYLSQ are shown. In the
first one all parameters are held constant except the
overall scale and g. In the second run all parameters are
allowed to refine.
-
Becker, P.J. and Coppens, P. 1974. Extinction within the Limit of Validity of the Darwin Transfer Equations. I. Refinement of Extinction in Spherical Crystals of SrF2 and LiF. Acta Cryst. A30, 148.
-
Buerger, M.J. 1960. Crystal Structure Analysis. New York: John Wiley.
-
Busing, W.R. and Levy, H.A. 1959. ORXLS, A Crystallographic Least-squares Refinement Program for the IBM 704. ORNL Report ORNL-CF 59-4-37
-
Finger, L.W. 1969. The Inclusion of Secondary Extinction in Least-Squares Refinement of Single-crystal X-ray Data. Yearbook 67. Carnegie Inst.Washington: 216.
-
Flack, H.D. 1983. On Enantiomorph-Polarity Estimation. Acta Cryst. A39, 876.
-
Larson , A.C. 1969. The Inclusion of Secondary Extinction in Least-Squares Refinement of Crystal Structures. Crystallographic Computing. F.R. Ahmed, S.R.Hall, C.P. Huber, eds., Munksgaard. Copenhagen: 291-294.
-
Waser, J. 1963. Least-Squares Refinements with Subsidiary Conditions. Acta Cryst. 15, 1091.
-
Zachariasen, W.H. 1967. A General Theory of X-Ray Diffraction in Crystals. Acta Cryst. 23, 558.
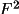
![\[
Q = \sum_{h} [w( Y_{o} - Y_{c} )^{2} ] = \sum_{h} [ w \Delta^{2} ]
\qquad \text{(summed over all hkl)}
\]](equations/4.19.1-eq-6.gif)
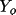
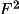
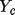
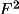
![\[F_{c} = A_{c} + i B_{c}\]](equations/4.19.1-eq-7.gif)
![\[
A_{c} = \sum_{n} [ \sum_{s} \{f_1 \cos \phi - f_2 \sin \phi \} ]
\]](equations/4.19.1-inf-1.gif)
![\[
B_{c} = \sum_{n} [ \sum_{s} \{f_1 \sin \phi + f_2 \cos \phi \} ]
\]](equations/4.19.1-inf-2.gif)
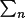
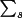
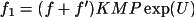
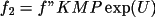
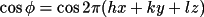
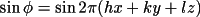
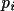
![\[
Q/dp_{i}= \sum_{r}[w \Delta dY_{c}/ dp_{i}] = 0 \]](equations/4.19.1-eq-8.gif)
![\[
Y_{c}= Y_{c}(0) + \sum_{j}[\epsilon_{j}dY_{c}/ dp_{j}] + H
\]](equations/4.19.1-eq-9.gif)
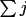
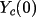
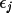
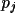
![\[
\sum_{r}[ wY_{o}- Y_{c}(0) -\sum_{j}\epsilon_{j}Y_{c}/dp_{j}) dY_{c}/ dp_{i}] = 0
\]](equations/4.19.1-eq-10.gif)
![\[
\sum_{r}[ w\sum_{j}( dY_{c}/dp_{i}\epsilon_{j}dY_{c}/dp_{j}] =
\sum_{r}[ w\sum_{j}( dY_{c}/dp_{i}\Delta ) ]
\]](equations/4.19.1-eq-11.gif)
![\(\sum_{j}[ A_{ij}\epsilon_{j}] = B_{i}\Delta \)](equations/4.19.1-eq-12.gif)
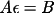
![\(A_{ij}= \sum_{r}[ w dY_{c}/dp_{i}dY_{c}/dp_{j}]\)](equations/4.19.1-inf-7.gif)
![\(B_{i}= \sum_{r}[ w dY_{c}/dp_{i}\Delta ]\)](equations/4.19.1-inf-8.gif)
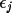
![\[
\rm{BCORR} = \epsilon(\rm{UOV}) - \epsilon'(\rm{UOV})
\]](equations/4.19.2.2-eq-14.gif)



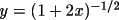
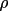
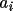
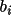
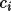
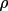
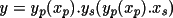
![\[
\Matrix{A}\epsilon= \Matrix{L}\Matrix{U}\epsilon =\Vector{B}
\]](equations/4.19.4-eq-15.gif)
![\[
\sigma_{i}= {A_{ii}^{-1}\sum_{r}[w \Delta ^{2}]/(n - m)}^{1/2}
\]](equations/4.19.5-inf-9.gif)
![\[
dF/dp_{j}= \sum _{i}[fct(i) dF/dp_{i}]
\]](equations/4.19.8.1-eq-16.gif)
![\[
\sigma p_{i}= {\sum _{j}[ \sum _{k}[fct(j) fct(k) COV(j,k) ] ]
\sum _{r}[w\Delta ^{2}]/(n-m) }^{1/2}
\]](equations/4.19.8.1-eq-17.gif)
![\[
\sum _{n}w_{n}(\Phi _{n}- \Phi _{n}obs)^{2}\]](equations/4.19.10-inf-10.gif)
![\[
w_{n}= \sum_{r}[w \Delta ^{2}] / (n-m) * 1 /\sigma ^{2}\phi_{n}
\]](equations/4.19.10-inf-11.gif)
![\[
F = \sum _{n}[(A/F)(A' - B") + (B/F)(B' + A")] = \sum _{n}F_{n}b
\]](equations/4.19.18-inf-12.gif)
![\[
A' = \sum _{s}[f_1 cos \phi ] B' = \sum _{s}[f_1 sin \phi ]
\]](equations/4.19.18-inf-13.gif)
![\[
A" = \sum _{s}[f_2 cos\phi ] B" = \sum _{s}[f_2 sin\phi ]
\]](equations/4.19.18-inf-14.gif)
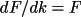
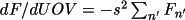
![\(
dF/df' = \sum _{n'}[f_1 /(f+f') ((A/F)A' + (B/F)B')]\)](equations/4.19.18.3-inf-17.gif)
![\(
dF/df" = \sum _{n'}[f_2 / f'' ((-A/F)B" + (B/F)A")]\)](equations/4.19.18.3-inf-18.gif)
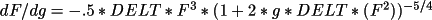
![\(
dF/dx = 2\pi h [(-A/F)(B' + A") + (B/F)(A' - B")]\)](equations/4.19.18.5-inf-20.gif)
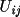
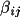
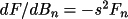
![\(dF/d(\beta _{ij})_{n}= h^{2}[(-A/F)(A' - B") - (B/F)(B' + A")]\)](equations/4.19.18.6-inf-22.gif)