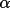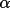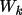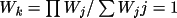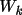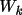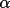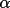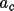|
| phase | m |
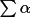
|
| - | 5 | 20 |
| +A | 3 | 15 |
| -AD | 2 | 10 |
where m is the number of invariants, this would lead to the correlation statistics
| phase = 0 (+) | frequency | Product of
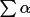 |
| -A | 1 | 300 |
| +AD | 1 | 200 |
| -D | 1 | 150 |
This process assumes that different symbol indications for the same reflection are in fact equal and may therefore be correlated. The statistics above are consistent with symbols A and B having the value of 180°.
The symbol correlation table is then used to test the plausibility of numeric values for each symbol. Symbols assigned to restricted phases are assigned their two possible values (e.g. p/2 and 3p/2) and symbols assigned to unrestricted phases are tested for the numeric values in the range 0 to 2p in intervals of p/4. The correlation statistics are used to calculate a correlation factor QFAC (Schenk, 1971) that has a maximum value of 100 if the numeric phases agree exactly (and -100 if they disagree exactly!). In space groups with translational symmetry (non-symmorphic) cofactors greater than 50 are good, and >70 are excellent. However, in the other space groups the QFAC is less indicative.
The last part of this step orders the phase sets in descending magnitude of cofactor. Only the top phase sets (16, or specified by user) will enter into the more exhaustive figure-of-merit tests in the next step.
The previous step selected, and ordered, the numeric phase combinations that have the best chance of being correct. In this step each of these combinations is applied in a separate symbolic addition cycle to provide the agreement statistics needed to calculate various figures-of-merit. A figure-of-merit is intended to discriminate between a 'good' phase set and a 'bad' phase set (i.e. one that may provide a correct solution from one that will not). Not all FOM's of the original SIMPEL versions are implemented at this time, but will be considered for future development. On the other hand, several FOM's have been added that are not present in the other SIMPEL versions.
This figure-of-merit is a reformulation of QFAC calculated in Step 4. It is
QFOM = 1.5 - QFAC/100.
In accordance with all other FOM values, the best QFOM is the lowest. It has an active range from 0.5 to 2.5, and any value below 1.1 is considered good, and above 1.5 is considered unlikely. QFOM is, of course, correlated to the symbol extension process and cannot be considered an independent phase set discriminator in the same sense as the FOM tests PSI0 and NEGQ. Caution must therefore be exercised in interpreting small differences in QFOM values.
This parameter is the inverse of the CFOM parameter of the MULTAN program (Main et al., 1980) and has the form
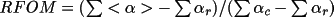 (summed over all
h)
(summed over all
h)
where
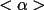 is the
expected
is the
expected
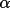 of a phase, and
of a phase, and
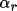 is the
is the
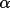 if all phases
were randomly distributed. For a correct phase set the
value of
if all phases
were randomly distributed. For a correct phase set the
value of
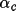 should approach that of
should approach that of
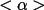 and RFOM
should tend to 1.0. Incorrect phase sets will deviate
significantly from 1.0, random phases towards 2.0, and
overcorrelated phases towards 0.0. In general, however,
phase sets with small RFOM's are more likely to be
correct than those with large RFOM's. The range of RFOM's
will vary according to the validity of the estimate of
and RFOM
should tend to 1.0. Incorrect phase sets will deviate
significantly from 1.0, random phases towards 2.0, and
overcorrelated phases towards 0.0. In general, however,
phase sets with small RFOM's are more likely to be
correct than those with large RFOM's. The range of RFOM's
will vary according to the validity of the estimate of
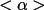 . For
this reason RFOM tends to be less reliable for strongly
non-random structures.
. For
this reason RFOM tends to be less reliable for strongly
non-random structures.
The RFAC parameter is similar to the residual FOM calculated in MULTAN (Main et al., 1980) except for a scale that takes into account the relative dominance of heavy atoms in the structure.
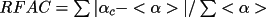 (summed over all
h)
(summed over all
h)
RFAC is a minimum when there is close
correspondence between
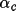 and
and
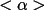 . In
this respect it is very similar to the R-factor of Karle
and Karle (1966). RFAC is, like RFOM, dependent on the
reliability of <
. In
this respect it is very similar to the R-factor of Karle
and Karle (1966). RFAC is, like RFOM, dependent on the
reliability of <
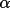 >.
>.
PSI0 triplet invariants (Cochran and Douglas,1955)
provide a figure-of-merit which is largely independent of
the triplet and quartet invariants used in the tangent
refinement. A PSI0 triplet relates two strong reflections
(with |E| > EMIN) to a third which has an |E|-value as
close as possible to zero (see the
GENSIN
writeup). The phases estimated from a series of
PSI0 triplets are expected to be random when the
contributing phases from the other two large-|E|
reflections are correct. When this is the case the
resulting values of
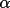
 are significantly lower than if the distribution
of contributing phases was biased or incorrect. These
invariants are used to form the figure-of-merit
are significantly lower than if the distribution
of contributing phases was biased or incorrect. These
invariants are used to form the figure-of-merit
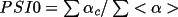 (summed over psi0
triplets ).
(summed over psi0
triplets ).
PSI0 should be smallest for the correct phase set. PSI0 is, along with NEGQ, one of the most independent methods of measuring the relative likelihood of success.
Quartet structure invariant relationships are classified according to the magnitude of their crossvector |E| values. When the crossvector |E|'s are small there is a high probability that the phase invariant has a value close to p rather than 0 (Hauptman, 1974; Schenk, 1974). These invariants are referred to as negative quartets. In SIMPEL negative quartets are not used in the phasing process but are retained as a test of the phase sets. The negative quartets are considered independent because, unlike the positive quartets, they cannot be represented by a series of triplet invariants. They provide, therefore, a separate estimate of the phases. A direct comparison of these phases provides the basis for the figure-of-merit (Schenk, 1974).
![\(NEGQ = \sum [ \alpha _{c}|\phi _{k}- \Phi _{k}| ] / \sum \alpha _{c}\)](equations/4.63.6.5-inl-1562.gif) (summed over all k neg.
quartets)
(summed over all k neg.
quartets)
where
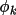 is the phase estimated
from triplets and positive quartets, and
is the phase estimated
from triplets and positive quartets, and
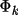 is the phase estimated
from negative quartets alone. Correct phase sets should
have low values of NEGQ ranging from 0 for
centrosymmetric structures, to 20-
is the phase estimated
from negative quartets alone. Correct phase sets should
have low values of NEGQ ranging from 0 for
centrosymmetric structures, to 20-
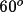 for
non-centrosymmetric structures. Note that if fragment
QPSI values are used the value of
for
non-centrosymmetric structures. Note that if fragment
QPSI values are used the value of
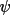 is automatically
set to 0 and the NEGQ test will remain valid. This FOM is
a very powerful discriminator of phase sets provided that
sufficient negative quartets are available.
is automatically
set to 0 and the NEGQ test will remain valid. This FOM is
a very powerful discriminator of phase sets provided that
sufficient negative quartets are available.
The combined FOM is a scaled sum of the FOM parameters QFOM, RFOM, RFAC, PSI0 and NEGQ.
![\(CFOM =\sum [WFOM_{i}(FOMMAX_{i}-FOM_{i})/ (FOMMAX_{i}-FOMMIN_{i})]\)](equations/4.63.6.6-inl-1567.gif) (i=1 to 5)
(i=1 to 5)
The weights WFOM may be specified on the SETFOM control line. These values are subsequently scaled so that the maximum value of CFOM is 1.0. It is important to emphasise that CFOM is a relative parameter and serves only to highlight which is the best combination of FOM's for a given run. It does not indicate if a given FOM will provide a solution.
The AMOS parameter is a structure-independent gauge of the correctness of a phase set. It uses pre-defined estimates of the optimal values for the FOM parameters QFOM, RFOM, RFAC, PSI0 and NEGQ. OPTFOM values may be user defined (see setfom line). Rejection values for the four FOM parameters are derived from the OPTFOM values as REJFOM = 3*OPTFOM. The default values are as follows:
| QFOM | RFOM | RFAC | PSI0 | NEGQ | |
| OPTFOM | 0.75 | 1.0 | 0.25 | .75 | 60° |
| REJFOM | 2.25 | 3.0 | 0.75 | 2.25 | 180° |
The absolute measure-of-success parameter is calculated from all active FOMs as
![\(AMOS = \sum [ WFOM_{i}( REJF_{i}- FOM_{i}/ OPTFOM_{i}]\)](equations/4.63.6.7-inl-1568.gif) (i=1 to 5)
(i=1 to 5)
where the WFOM values are scaled so that AMOS ranges from 0 to 100. In addition to being used to sort phase sets in order of correctness, the AMOS values provide a realistic gauge of the correctness of phase sets. As a rule of thumb, they can be interpreted in the following way:
| AMOS | |
| 100-81 | high probability of being correct set |
| 80-61 | good chance of being correct set |
| 60-41 | possibility of being correct set |
| 40-21 | low probability of being correct set |
| 20-0 | very unlikely to be correct set |
These classifications are only approximations. The predictability of optimal FOM values can be perturbed by a variety of structure dependent factors and by the FOM weighting.
Phase sets must satisfy certain criteria before being considered for possible output to the binary file for subsequent E-map calculations.
| FOM Rejection Criteria | Message |
| Reject if QFAC > REJFOM(1) |
REJECT1
|
| Reject if RFOM > REJFOM(2) |
REJECT2
|
| Reject if RFAC > REJFOM(3) |
REJECT3
|
| Reject if PSI0 > REJFOM(4) |
REJECT4
|
| Reject if NegQ > REJFOM(5) |
REJECT5
|
| Reject if |av.φ-<av.φ>| > 45° |
REJECT10
|
The value of
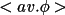 is
90° for centrosymmetric structures and
150-180° for non-centrosymmetric structures. This
test avoids the "all-plus catastrophe" phase set.
is
90° for centrosymmetric structures and
150-180° for non-centrosymmetric structures. This
test avoids the "all-plus catastrophe" phase set.
-
Reads |E| values from the input archive bdf
-
Writes the estimated phases to the output archive bdf
-
Reads structure invariant relationships from bdf
inv
SIMPEL
This is the standard run in which all defaults will
be applied to the converge, diverge, symbolic addition and
FOM testing processes. All |E|-values used in the
GENSIN
program, and all invariants entered on
inv, will be applied
in the phasing process. Phase extension will be based on
weighted
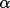 s.
s.
SIMPEL 60 200 *6 8 :set con/divergence limits
invar all 1. 0.7 :use all invariants with new a/b limits
start trip :use only triplets in converge process
symbad an single :accept single symbols based on altm
print bdfout :print phase sets output to bdf
SIMPEL symbad wa single :use weighted alphas ; reject multisymbols phase 5 7 11 0 nul :suppress from process phase 1 2 7 :assign as symbolic phase
-
Cochran, W. and Douglas, A.S. 1955. Proc. Roy. Soc. A277, 486-500.
-
Germain G., Main, P. and Woolfson, M.M. 1970. Acta Cryst. B26, 274-285.
-
Hauptman, H.A. 1974. Acta Cryst. A30, 472-476.
-
Karle, J. and Karle, I.L. 1966. Acta Cryst. 21, 849.
-
Karle, J. 1974. International Tables , Vol. IV, section 6, 337.
-
Main, P. 1980. Multan-80 York England: University of York. Overbeek, A.R. & Schenk, H. 1978. Computing in Crystallography, University Press, Delft, p108-112.
-
Schenk, H. 1971. Acta Cryst. B27, 2037-2039.
-
Schenk, H. 1974. Acta Cryst. A30, 477-481.
-
Schenk, H. 1980. Computing in Crystallography, eds. R. Diamond, S. Rameseshan and K. Venkatesan, Indian Academy of Sciences, Bangalore, p701-722.
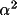
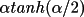
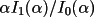
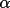
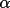
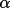

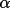
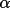
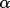
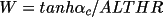
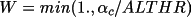
![\(alpha;_{c}= [ {\sum W_{k}\alpha _{k}sin \phi _{k}}^{2}+ { \sum W_{k}\alpha _{k}cos \phi _{k}}^{2}]^{1/2}\)](equations/4.63.4.1-inl-1532.gif)