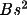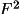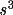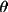|
| Expected mean of | <|E|> | <|
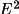 |> |> |
<|
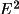 -1|> -1|> |
<|
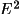 -1| -1|
 > > |
<|
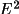 -1| -1|
 > > |
| For random P -1 | .798 | 1.000 | .968 | 2.000 | 8.000 |
| For random P 1 | .886 | 1.000 | .736 | 1.000 | 2.000 |
| Percent of Total With |E|> | 0.0 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.50 | 3.00 |
| For random P 1 | 100. | 31.7 | 23.0 | 16.1 | 11.0 | 7.2 | 4.6 | 1.20 | 0.27 |
| For random P 1 | 100. | 36.8 | 23.7 | 14.1 | 7.7 | 3.9 | 1.8 | 0.19 | 0.01 |
GENEV provides for two basic scaling approaches: The
linear scale Kexp(8
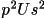 ) (this is the
default) and the profile scale (
) (this is the
default) and the profile scale (
). In addition there are two rescaling
procedures; overall (default) and index (using
indexk ). The definitions
and the properties of these scales is detailed by S & H
(1982).prof
The application of the linear scale first requires the evaluation of the overall scale, K, and the overall thermal parameter U from the Wilson plot. The particular form of the linear scale used to calculate |E1| is based on U and K values estimated using a inflection-point least-squares procedure (see below). Use of the linear scale is optional for |E2| and, if applied in the default mode, will be identical to that used for |E1|. Entering the frag line will cause an independent linear scale to be evaluated for |E2|.
If a
is entered on the GENEV line the profile
scale is used to evaluate |E2|. The profile scale is an
interpolated curve based on 41 overlapped Wilson plot
averages. Some degree of caution should be exercised in
using this option because of the tendency of the
radially-dependent structural contributions to |E2| to be
reduced. It may, however, be useful for reducing the
dominant features such as occur in "chicken-wire"
structures.prof
The rescaling options in GENEV are used to insure
that the overall mean |
 | is precisely one.
The simplest and most effective way of achieving this is
by summing the |E| values determined using linear or
profile scales, and then applying the inverse of the
average |
| is precisely one.
The simplest and most effective way of achieving this is
by summing the |E| values determined using linear or
profile scales, and then applying the inverse of the
average |
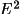 |. This is referred
to as overall rescaling. It is mandatory for |E1| and
optional for |E2|.
|. This is referred
to as overall rescaling. It is mandatory for |E1| and
optional for |E2|.
With index rescaling, different groups of
reflections defined by a particular combination of hkl
indices are rescaled so that the mean value of |
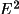 | is one. This
option may be applied only to |E2|. The conditions for
each index group may be specified on the
indexk line with the 15
parameters
| is one. This
option may be applied only to |E2|. The conditions for
each index group may be specified on the
indexk line with the 15
parameters
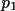 ,
,
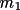 ,
,
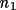 ,
,
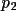 , . . .
, . . .
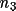 . A reflection belongs
to a particular index group provided its indices jointly
satisfy the following three equations:
. A reflection belongs
to a particular index group provided its indices jointly
satisfy the following three equations:
![\([ h p_{1}+ k q_{1}+ l r_{1}]mod(m_{1}) = n_{1}\)](equations/4.25.3.4-inl-872.gif)
![\([ h p_{2}+ k q_{2}+ l r_{2}]mod(m_{2}) = n_{2}\)](equations/4.25.3.4-inl-873.gif)
![\([ h p_{3}+ k q_{3}+ l r_{3}]mod(m_{3}) = n_{3}\)](equations/4.25.3.4-inl-874.gif)
Each group may be specified by a separate
indexk line or, in the
case of the even-odd parity groups, with a single blank
indexk line. Only the
specified index groups will be scaled separately, the
remainder will be scaled together. Judicious use of the
index parameters will permit single reflections to be
scaled in this way. Specific scale values may also be
entered on the
indexk line for this
purpose. No attempt will be made to make the mean |
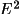 | = 1. in this
case.
| = 1. in this
case.
The index rescaling option must also be used carefully. As with the profile scale it can have the overall effect of reducing the structural content of the |E| values. The study of S & H (1982) showed that, in general, it provided less reliable |E|s than the overall rescaling option. Index rescaling can, however, be useful in the study of superstructure or hypersymmetry, since it ensures that groupings of reflections are given similar weight in the phasing process.
A squared normalized structure factor is the ratio of
its scaled intensity to its expectation value. The
expectation value for an intensity (or rather |
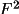 |) depends on what is
known about the structure. If only the atomic contents of
the unit cell are known, then the best estimate of <
|) depends on what is
known about the structure. If only the atomic contents of
the unit cell are known, then the best estimate of <
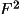 > is the
random-atom approximation (see S & H, 1982, for
definition). Using the random-atom <
> is the
random-atom approximation (see S & H, 1982, for
definition). Using the random-atom <
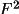 > in the
normalization process provides |E| values that will reflect
how well the |F| values conform to those expected for a
random structure. Significant departures of individual |
> in the
normalization process provides |E| values that will reflect
how well the |F| values conform to those expected for a
random structure. Significant departures of individual |
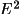 | values from 1.0 (the
overall mean) indicate whether a reflection is sensitive to
the non-random aspects of the structure. The larger the
departure from 1.0, the more important that reflection will
be to a phasing process designed to investigate the
non-random aspects of a structure. This is the basis for
most structure invariant procedures.
| values from 1.0 (the
overall mean) indicate whether a reflection is sensitive to
the non-random aspects of the structure. The larger the
departure from 1.0, the more important that reflection will
be to a phasing process designed to investigate the
non-random aspects of a structure. This is the basis for
most structure invariant procedures.
If the coordinates of a structure are known (i.e.
refined) then the value of <
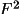 > is simply
calculated |
> is simply
calculated |
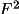 |, assuming
atoms-at-rest. Application of this expectation value in the
normalization procedure will result in all |
|, assuming
atoms-at-rest. Application of this expectation value in the
normalization procedure will result in all |
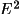 | values being close
to 1.0 (assuming of course, good data and a well-refined
structure). Obviously |E| values determined in this way are
of very limited use in direct methods since all reflections
have equal weight. Those that are most sensitive to the
non-random aspects of the structure cannot be
identified.
| values being close
to 1.0 (assuming of course, good data and a well-refined
structure). Obviously |E| values determined in this way are
of very limited use in direct methods since all reflections
have equal weight. Those that are most sensitive to the
non-random aspects of the structure cannot be
identified.
Contrasting the application of random-atom and
refined-atom expectation values illustrates a very
important aspect of the normalization process. Structure
information used in the expectation value will reduce that
particular contribution in the resulting |E| values. In
other words, the departures of |
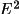 | values from unity
reflect the differences due to structural information not
used in evaluating the expectation value. In general,
therefore, the higher-order expectation values, as provided
with fragment information of type 2, 3, and 4 (see below),
often have deleterious effects on the calculation of |E|
values. There will, however, be situations when selective
attenuation of structural information from |E| values, via
the application of high-order expectation values, is
extremely useful. The reduction of the dominant effects of
a heavy atom or planarity are two obvious examples. In
general, however, it is strongly recommended (S & H,
1982) that the random-atom expectation value be used in the
initial stages of a structure solution, even when
additional structure information is known (note well the
comments in the next section).
| values from unity
reflect the differences due to structural information not
used in evaluating the expectation value. In general,
therefore, the higher-order expectation values, as provided
with fragment information of type 2, 3, and 4 (see below),
often have deleterious effects on the calculation of |E|
values. There will, however, be situations when selective
attenuation of structural information from |E| values, via
the application of high-order expectation values, is
extremely useful. The reduction of the dominant effects of
a heavy atom or planarity are two obvious examples. In
general, however, it is strongly recommended (S & H,
1982) that the random-atom expectation value be used in the
initial stages of a structure solution, even when
additional structure information is known (note well the
comments in the next section).
The general problem of applying known structural information to the structure invariant process is described by Main (1976). The definitions of the different categories of structural information as used by GENEV have been detailed by S & H (1982). These are treated in GENEV as the following categories,
| type 1 is for random atoms | (
on
line) |
| type 2 is for random fragments | (
on
line) |
| type 3 is for oriented fragments | (
on
line) |
| type 4 is for positioned fragments | (
on
line) |
While fragment information of type 2, 3, and 4 may
not provide |E2| values that are more reliable than |E1|
values based on random-atom expectation values, it should
always be included in the GENEV calculation when
available. This is because the group structure factors
which are calculated as part of the evaluation of the
expectation value of F squared, <
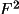 >, provide phase
information that is extremely useful in subsequent stages
of the phasing process. This phase information can be
applied to |E1|, as well as |E2|, in later
calculations.
>, provide phase
information that is extremely useful in subsequent stages
of the phasing process. This phase information can be
applied to |E1|, as well as |E2|, in later
calculations.
For a random-atom structure, the Wilson plot is a
straight line defined by the overall thermal displacement
parameter of the constituent atoms, and the overall scale
of the measure structure factors. For a real structure, a
Wilson plot will often show significant systematic
deviations from this line due principally to the
short-range interatomic distances in the structure. The
scattering effects of translational symmetry on the radial
distribution of intensities is known as Debye scattering.
For the majority of light-to-medium atom structures, the
gross effects of Debye scattering are very similar. For
instance the nodes, antinodes and inflection-points of a
Debye scattering curves calculated for interatomic
distances ranging from 1.30 to 1.55A in a 6-membered ring
molecule are quite similar (H & S, 1982a). This means
that for many structures inflection-points (the points
where the Debye curve crosses the linear mean line) provide
a means of finding a reliable linear fit to the Wilson
plot, independent of the extent of the Debye scattering
effects and the
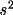 truncation of the
data.
truncation of the
data.
GENEV uses the Wilson plot ratios for the 5 ranges
clustered about the two cardinal inflection-points. The s
squared default values for these inflection-points are set
at 0.15 and 0.26
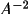 , but these may be
changed for non-typical structures with the
, but these may be
changed for non-typical structures with the
and
din1
input on the GENEV line. In addition to the
clusters of 5 points fixing the two inflection-points, the
five largest Wilson plot ratios are used to fix the low
angle part of the least-squares line. The user should
always check that the assumptions embodied in the
inflection-point least-squares process are valid for each
structure. The Wilson plot points used for this purpose are
shown in the printed graph as at signs (
@ ). It is recommended that
GENEV be rerun with specified values of U and K (using the
din2
and
fixu
options) or different inflection-points
(using
fixk
and
din1
values), if the least-squares fit is
unsatisfactory.din2
GENEV provides an estimate of the |E(hkl)| errors
using a procedure described by H & S (1982b). The
principal source of error in |E| values arises from
inaccuracies in the measured structure factors. It follows
that the legitimacy of the errors estimated in GENEV will
depend on the precision of the
 F values entered
on the bdf. The second most important contributor to the
|E(hkl)| errors arises from fitting the linear or profile
scaling functions to the Wilson plot (see below). The
effect of Debye scattering on the Wilson plot has already
been discussed, and this is taken into account when
estimating the errors. The errors estimated for |E1| and
|E2| are placed in the bdf for use in subsequent
calculations. The error distribution for a typical
structure is listed below.
F values entered
on the bdf. The second most important contributor to the
|E(hkl)| errors arises from fitting the linear or profile
scaling functions to the Wilson plot (see below). The
effect of Debye scattering on the Wilson plot has already
been discussed, and this is taken into account when
estimating the errors. The errors estimated for |E1| and
|E2| are placed in the bdf for use in subsequent
calculations. The error distribution for a typical
structure is listed below.
| Error for |E|s > | 0.00 | 1.00 | 1.20 | 1.40 | 1.60 | 1.8 | 2.0 | 2.5 | 3.0 |
| |E| from linear K | .25 | .60 | .70 | .80 | .90 | 1.0 | 1.1 | 1.3 | 1.5 |
| |E| from profile K | .30 | .65 | .75 | .85 | .90 | 1.0 | 1.1 | 1.3 | 1.5 |
Error at mean
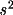 = =
|
.00 | .05 | .10 | .125 | .150 | .175 | .200 | .225 | .250 |
| |E| from linear K | .15 | .17 | .19 | .21 | .22 | .27 | .32 | .35 | .38 |
| |E| from profile K | .20 | .20 | .25 | .36 | .26 | .30 | .31 | .33 | .37 |
The user may decide which GENEV items are output to
lrrefl:
of the bdf. If an
archiv line is not
entered, the following items are automatically output to
the bdf.
| Scales K | (item 100-) | in record
lrexpl:
|
| Overall U | (item 2) | in record
lrdset:
|
| Fragment count | (item 10) | in record
lrdset:
|
| |E1| | (item 1600) | in record
lrrefl:
|
| |E2| | (item 1601) | . . . . . . |
| σ|E1| | (item 1602) | . . . . . . |
| σ|E2| | (item 1603) | . . . . . . |
| Group structure factor 1 | (item 1606) | . . . . . . |
| Group structure factor 2 | (item 1607) | . . . . . . |
| . . . . . . . . | . . . . | . . . . . . |
| Group structure factor N | (item 1605+N) | . . . . . . |
If any
archiv lines are entered,
the items 1600 to 1630 must be named explicitly to be
output to the bdf. Particular care must be taken if
fragment information is used in GENEV calculation. The
number of group structure factors (items 1606 on) is equal
to the number of fragments, except for type 3 fragments
where there is one group structure factor for each point
group. The user must also check if any extra type 1
fragments have been added by GENEV to balance the cell
content. Subsequent calculations that use the group
structure factor phases require that the correct number be
present. It is important to note that if GENEV items 1600
to 1630 are present on the input bdf, they will not be
transferred to the output bdf. These are purged from
lrrefl:
before new GENEV items are appended. Additional
items, other than 1600 - 1630, may also be deleted from
lrrefl:
using the
archiv lines. A maximum
of 30 items may be added or deleted in this way.
Tip 1 Check that sin
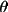 /
/
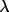 maximum on the
GENEV line is as accurate
as possible. The default value comes from the bdf,
otherwise it is set to 1.0. If
maximum on the
GENEV line is as accurate
as possible. The default value comes from the bdf,
otherwise it is set to 1.0. If
ADDREF
has been used with the two pass option, the accurate
value will be stored.
Tip 2 Assess the precision
of the data. If some weak data are missing from the input
bdf, use the
option to compensate for this. If the weak
data have not been processed with Bayesian statistics
(e.g.negative |
fill
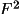 | have been set to 0),
then the
| have been set to 0),
then the
option can be used to apply a limited
Bayesian treatment to |F| and
baye
 F values.
F values.
Tip 3 Check what scaling and expectation options should be applied in the calculation of |E2|. These are fixed for |E1|.
Tip 4 If the values of
either U or K need to be fixed, use the
and/or
fixu
options. These will apply only to
|E2|.fixk
Tip 5 The default rescaling
mode for |E2| is index rescaling applied to the eight
parity groups, provided that
frag,
, or
prof
options are not used. If any of these lines
are entered, the default rescaling mode for |E2| becomes
'overall'. Index rescaling may be specified explicitly with
the
indexk line(s) but care
should be taken in selecting index groups appropriate to
the problem.fixu/k
Tip 6 Known structure information is entered using the frag, site, sitea, and siteg lines. Fragment information is entered for the asymmetric unit, as opposed to the celcon information which is entered for the whole cell. sitea lines containing coordinates in orthogonal Angstroms must be used for type 2 fragments. A grid line must precede the first siteg line entered. The frag line may be used to move the origin of atom coordinates that follow. This is sometimes useful for converting from type 3 to type 4 input.
Tip 7 The user may output
the |
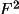 | expectation values
used in the GENEV calculation as items 1604 and 1605 in
| expectation values
used in the GENEV calculation as items 1604 and 1605 in
lrrefl:
. This can be efficient for very large
structures when GENEV is repeated for different
normalization parameters but the same fragment information.
This is specified by putting
in the
GENEV line and leaving
out the
frag and
site lines.bexp
Tip 8 Cell content
information is extracted from the input bdf (if entered
through the program
STARTX
). This may be replaced by entering
celcon lines.
Tip 9 Always check that the
items to be used in subsequent calculations (e.g.
GENSIN
,
GENTAN
, and
FOURR
) are to be output. In most cases the default items
will be sufficient, but in special cases the
archiv line(s) can be
used to add the items required. It is good archival
practice to regularly check the contents of
lrrefl:
and remove any items that are no longer
needed.
-
Reads structure factors from the input archive bdf
-
Writes normalized structure factors (E's) to the output archive bdf
GENEV smax 0.52 :s max of all data is .52
|E1| will be calculated with linear scale,
random-atom expectation value, and overall rescale. |E2|
will be the same except for index rescaling using hkl
parity groups. No |E| values will be listed and |E1| and
 |E1| will be
output on the bdf.
|E1| will be
output on the bdf.
GENEV list 1.5 frag oriented :specify type 3 fragment site br1 .5 .5 0 *7 .5 :bromine in special position site c1 .73 .57 .333 site n3 -.15 .44 .62 archiv 1600 1602 1606 1607 :add |E1|, s|E1|, gsf1, gsf2
|E2| will be calculated with a linear scale, overall rescale and an expectation value derived from the type 3 fragment of atoms Br1, C1, and N3 and the remaining atoms (i.e. balance of cell contents) as a type 1 fragment.
GENEV smax .33 fixu .04 baye fill indexk :use index rescale (parity hkl) for |E2| archiv 1601 1603 -1800 :add |E2|, sigma|E2|, delete |Fc| from bdf
|E2| will be calculated with linear scale (with
u=0.04), random-atom expectation value, and index rescaling
with parity groups. All input |F|s and
 |F|s are treated
with limited Bayesian statistics and the Wilson plot is
adjusted for missing data. Only |E2| and
|F|s are treated
with limited Bayesian statistics and the Wilson plot is
adjusted for missing data. Only |E2| and
 |E2| are added to
the bdf; |Fc| is removed.
|E2| are added to
the bdf; |Fc| is removed.
GENEV dset 3 bexp prof indexk 1 1 1 4 1 :set index scale group 1 indexk 1 1 1 3 *16.5 :set index scale group 2 and set scale
|E2| will be calculated with a profile scale, random-atom expectation value, and index rescaling based on the groups (h+k+l)mod4=1, (h+k+l)mod4=3, and the remainder. The scale of the second index groups will be fixed at 0.5. In this example the two |E| estimates will be output without their error values.
-
French, S. and Wilson,K. 1978. On the Treatment of Negative Intensity Observations. Acta Cryst. A34, 517-525.
-
Hall, S.R. and Subramanian V. 1982a. Normalized Structure Factors. II. Estimating a Reliable Value of B . Acta Cryst., A38,590-598.
-
Hall, S.R. and Subramanian,V. 1982b. Normalized Structure Factors. III. Estimation of Errors . Acta Cryst. A38, 598-608.
-
Luger, P. 1980. Modern X-ray Analysis on Single Crystals. New York: de Gruter.
-
Main, P. 1976. Recent Developments in the MULTAN System - The Use of Molecular Structure.. Crystallographic Computing Techniques, F.R. Ahmed, K. Huml, B. Sedlacek, eds., Munksgaard. Copenhagen: 97-105.
-
Stout, G.H. and Jensen,L.H. 1968. X-ray Structure Determination: A Practical Guide : New York: MacMillan.
-
Subramanian, V. and Hall, S.R. 1982. Normalized Structure Factors. I. Choice of Scaling Function. Acta Cryst. A38, 577-590.
-
Wilson, A.J.C. 1942. Determination of Absolute from Relative X-ray Intensity. Nature 150, 151-152.