Authors: H. Wang, R.J. Barton
and B.E. Robertson
Contact: Bev Robertson,
Department of Chemistry, University of Regina, Regina,
Saskatchewan, Canada S4S 0A2
REGFE calculates crystallographic functions and
their estimated standard deviations (Busing et al., 1964).
In the calculation of standard deviations, both the
variances and the covariances of the parameters (Hamilton,
1964; Sands, 1982) are taken into account. REGFE may be
used to create tables of bond lengths, bond angles and
dihedral angles for publication and output them to the
'punch' file.
REGFE calculates the values of derived quantities
which are functions of the atomic coordinates and the
crystal unit cell parameters and their associated standard
deviations. These quantities are bond lengths, bond angles,
dihedral angles, distances of atoms from planes and lines,
and angles between planes and lines. The calculations of
bond lengths, angles and dihedral angles of molecules or
clusters can be performed, based on atom
connectivity.
In least-squares structure refinement, the parameters
of the crystal structure are not fully independent of each
other; i.e., they are correlated. For any function of these
parameters the covariances of the parameters should be
included in the calculation of their standard
deviation.
There are two variance-covariance (v-c) matrices
which are involved in the calculation of the standard
deviation; the matrix, C, of the cell parameters and the
matrix, V, of the atom parameters. We assume that the cell
parameters are fully independent of the atom parameters and
the covariance terms involving a cell parameter and an atom
parameter are set to zero.
The variance-covariance matrix of the atom parameters
is derived from the inverse matrix of the normal matrix in
least-squares refinement. If the weights for the
observations (F,
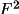 or I) are correct, V
is the inverse of the normal matrix. However, it is assumed
that any deviations of the goodness-of-fit, S, from its
expected value represent a scaling error in the variances
of the observations, and thus can be corrected by
multiplying V by
or I) are correct, V
is the inverse of the normal matrix. However, it is assumed
that any deviations of the goodness-of-fit, S, from its
expected value represent a scaling error in the variances
of the observations, and thus can be corrected by
multiplying V by
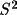 ; i.e.
; i.e.
V =
A
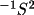
where
A is the normal matrix of
the least-squares refinement, given by
![\(A_{ij}= \sum _{r}[ w dF_{{\rm cal}}/ dp_{i}dF_{{\rm cal}}/ dp_{j}]\)](equations/4.54.1-inl-1417.gif)
and S, the goodness-of-fit is given by
![\(S^{2}= \sum _{r}[w\Delta ^{2}] / (n-m)\)](equations/4.54.1-inl-1418.gif)
The symbols and notation in these equations have been
defined in the CRYLSQ section.
The diagonal terms of the v-c matrix are the
variances of the parameters and the off-diagonal terms are
the covariances of the parameters. The correlation matrix,
N, of the atom parameters is a normalized
variance-covariance matrix. The elements of the correlation
matrix are defined as:
![\(N_{ij}= V_{ij}/ [ V_{ii}V_{jj}]\)](equations/4.54.1-inl-1419.gif) (i,j =
1,2,3,...,m)
(i,j =
1,2,3,...,m)
The correlation matrix of the atom parameters can be
created and saved in the bdf
cmx
by entering the
ms
option code in CRYLSQ. Thus at least one
cycle of least-squares refinement by CRYLSQ is required
before running REGFE. If the correlation matrix from
least-squares structural refinement is a blocked matrix,
the parameters in different blocks are considered to be
uncorrelated and the covariances of parameters in two
different blocks will be set to zero. If the correlation
matrix is not provided, only the variances of the
parameters will be used and all the covariances of the
parameters will be set to zero.
Standard Deviation Calculation
For a given crystallographic function of the atom
parameters a1, a2, a3, ..., and cell parameters c1, c2, c3,
...
F = f(a1, a2, a3, ..., c1, c2, c3, ..., c6)
the variance (which is the square of the standard
deviation, sigma) of the function can be obtained by
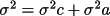
The first term in the right hand side of the equation
is the contribution to the variance of the function from
the variances of the unit cell parameters:
![\(\sigma ^{2}c = \sum _{ij}[ C_{ij}dF/dc_{i}dF/dc_{j}]\)](equations/4.54.2-inl-1421.gif)
and the second term is the contribution to the
variance of the function from the variances of the atom
parameters:
![\(\sigma ^{2}a = \sum _{ij}[ V_{ij}dF/da_{i}dF/da_{j}]\)](equations/4.54.2-inl-1422.gif)
The atom connectivity is established according to the
atomic radii data. The symmetry operations of the space
group may be applied for the establishment of the atom
connection table. The number (1, 27, 125) of unit cells can
also be specified for atom searching. The values of the
atomic radii must be provided from the input bdf or
atrad lines. The values
of the atomic radii in the bdf can be modified by entering
atrad lines. The min
allowed radius is 0.015 A.
In the function and error calculation, a plane can be
represented by either a plane ID, which is predefined in a
plane line, or by three
atom IDs which define the plane. A line can be represented
by either a line ID, which is predefined in a
line line, or by two atom
IDs which define the line. The equation of a plane can be
created by entering the coefficients of the plane equation
in either an orthogonal coordinate system or a fractional
coordinate system, or by three atom IDs. Similarly, the
equation of a line can be defined by entering the
coefficients of a line equation in either an orthogonal
coordinate system or a fractional coordinate system, or by
two atom IDs. The forms of the equations of a plane and a
line in factional coordinate system are given by:
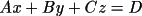
and
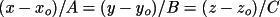
respectively. However, when the coefficients of the
equations are input on lines, only the variance of the
coefficients will be used in the standard deviation
calculations.
-
Optionally reads structure data from input
archive bdf
-
Optionally reads correlation matrix from bdf
cmx
-
Optionally outputs tables to line file
pch
In this example, the atomic radii of Zn and Cl are
modified and the bond lengths, bond angles, and dihedral
angles of the molecule will be calculated based on the atom
connectivity. The correlation matrix will be input from
cmx
and used in the standard deviation
calculations.
In this example, the calculation of the bond lengths,
angles and dihedral angles is suppressed. The covariance of
the atom parameter will be used in the standard deviation
calculation and the variance-covariance matrix will be
listed in the output.
-
Busing, W.R., Martin, K.O. and Levy, H.A. 1964.
ORFFE--Oak Ridge National
Laboratory, Report ORNL-TM-306.
-
Hamilton, W.C. 1964.
Statistics in Physical Science,
The Ronald Press Company: New York.
-
Sands, D.E. 1982.
Vectors and Tensors in
Crystallography, Addison-Wesley:
NewYork.