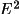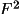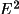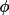A Fourier may be output in a compact form with the shaded option of the print line. Layers are printed with one column and one line per grid point. By judicious choice of the PRINTSCL constant and SCLINT density interval a shaded mini-Fourier can be produced which shows the structure on an approximately 1/4 scale when compared to the default maps. The peaks are represented by higher density print characters. Zero is represented by period, and the negative regions by a different set of characters. The actual coordinates of the peaks may be determined by the use of PEKPIK which processes the Fourier transform as it is stored on the mapfile.

An alternative column output is possible where base-36 arithmetic is used to give densities 0 through 9 and A through Z. This kind of printing is referred to as packed . No negatives are printed when this option is specified on the print line.

Ideally the limits of the Fourier transform should only encompass one asymmetric unit as close to the origin as possible. The default limits for the parallelepiped produced by the FOURR program attempt to achieve this goal. For the higher symmetry space groups it will often be necessary to produce more than an asymmetric portion of the cell since the limits set are always an integral number of grid points along the axial directions. When there is redundancy, the PEKPIK program will screen out the symmetrically equivalent points which have been produced. An algorithm has been set up which uses the space group symmetry operators to seek an asymmetric portion of the unit cell. These limits are those which are set when the default limits are utilized. The layout or map lines allow the user control of the limits of the map if it is desired to control these limits for other reasons. It should be noted that for small regions the BL algorithm may be the best choice since only the map specified will be calculated. It is necessary when using the FFT algorithm always to calculate a full cell span whether or not only a small fraction of the cell is written to the mapfile or to the line display device.

The summation order is usually determined by the axial lengths of the unit cell. When the long axis is summed first, the calculation will be fastest and the least computer memory will be required. Thus the default will be long axis layer to layer, next longest axis down each layer, and shortest axis across each page. Both the map and layout input lines allow the user a means to override these defaults by specifying the desired orientation of the map on the printed pages.

FOURR performs Fourier transforms on a wide range of coefficients and phase types. The coefficients and phases must be functions of the quantities stored in the input bdf. The most common coefficient types are selected by setting a signal in the FOURR input line. These are:

In addition to the pre-set transforms described above, the FOURR program uses of a coeff line to specify coefficients from constants and from quantities held in the bdf. This allows almost any type of transform to be undertaken with relative ease. In addition, the program BFOURR can be used to store very complex Fourier coefficients on the bdf, which may be employed in FOURR through the use of a coeff input line. This is discussed below.

In FOURR the user may explicitly define Fourier coefficients and phases using the coeff line. This is done with the identification (ID) numbers of items in the lrrefl: packet of the input bdf (for details see the BDF section at the back of this manual), and explicit constants. A coefficient is specified as a series of integers. Positive integers represent the ID numbers, negative integers represent positive constant scales, and zeros signal that a particular component is to be excluded from the construction of the Fourier coefficient. The general form of coefficient expression is as follows:

Coefficient = (factor1 * factor2 * scale3 - factor4) * factor5 * scale6

where the components factor1, factor2, factor4 and factor5 may be specified in fields 1, 2, 4 and 5 of the coeff line as ID numbers or constants. The components scale3 and scale6 must be specified as either the ID number of the scale group, or as a constant scale value.

The coefficient phase is defined using fields 7 and 8, or field 9. Fields 7 and 8 specify the real and imaginary components of the structure factor in terms of their ID numbers. Field 9 specifies the ID number of the structure factor phase in cycles. If both are specified and are present in the bdf the phase defined by field 9 will be used. These fields are applied to the Fourier expression as follows:

cos = factor7 / ((factor7) + (factor8) ) or cos = cos(2 factor9)

sin = factor8 / ((factor7) + (factor8) ) or sin = sin(2 factor9)

To illustrate the application of these coefficients in more general cases the six standard transforms specified via the FOURR line are shown as they would be defined on a coeff line. In the table which follows, n represents the dataset number.

It will be necessary to read the BDF section at the back of this manual, and in particular the part concerning the lrrefl: ID numbers, to understand properly how to use the coeff line. It is important to stress that to permit maximum flexibility there is very little internal checking of parameters input on the coeff line.

Output of the Fourier densities may be as a printed map or as a mapfile. The bdf serves as input to programs such as SLANT , PEKPIK , CONTRS . The quantities stored in this file include the generated transform, the description of the map, cell dimensions, and space group symmetry operations. The printed output is identical to the map output to the file but on a different scale, as described above. If the number of points in the third sum direction is more than can be printed across a page, the printed output may be abbreviated to accommodate the number of print columns on the printer. If it is abbreviated, the method leaves out alternate points thereby reducing the resolution of the printed map. All points are written to the mapfile.

The printed output may be scaled so that a distance on the page will have an Angstrom equivalent. No attempt is made, however, to compensate for the effect of an interaxial angle in the printed layer. The program CONTRS will produce a file for plotting of undistorted contour maps.

The output map of FOURR is divided into specific densities on a three dimensional grid. The grid interval, or rather the number of grid points along each cell dimension, defines the map resolution. Typically this resolution needs to be 3 or 4 points per Angstrom. In FOURR the default resolution is set at 0.25 Angstroms. This may be changed using a grid line. In conjunction with this option, it should be noted that the maxhkl line provides a means to reject reflections that do not contribute to the sums for the resolution specified by the given grid. In the case of the FFT method, the resolution specified will force the rejection of reflections beyond the resolution limit set or cause the inclusion of zero for those beyond the limit. An attempt to calculate a FFT with grid intervals of less resolution than the maximum h, k, l data allowed will result in an error termination.

The F(0,0,0) term is an important part of the Fourier calculation. The default F(0,0,0) term is applied for the following options:

These values may be replaced using the fzero input line.

FOURR patt ffsum
map *5 .5

This use of the Fourier program will result in a Patterson map being produced. The algorithm which is used for the second and third sums will be the FFT. The scale of the map will be four points per Angstrom. The summation will be made over the long axis first, so that there will be a number of pages corresponding to one layer every 1/4 Angstrom. If there is an interaxial angle in the plane of the "page" there will be a distortion due to the orthogonal print positions. The mapinput line forces the printing and limits the printing to 1/2 the cell in the first sum direction. The scale will default to one electron squared per Angstrom cubed for a Patterson map.

FOURR patt 
print *3 10 -100
map c 0 0 0 .25 1 .25

In this case, a Patterson function is to be computed. However, more control over the orientation, scale, and extent of the transform is desired. The algorithm used will be BL. The print line supplies directives to print the map, to scale to one electron squared per Angstrom cubed - assuming the F(rel) scale factor is reasonably close to one. If GENEV has been run, an estimate of the F(rel) scale factor will be known. Furthermore, the print line has a specification to suppress printing of all values between 10 and -100. This means that the map will have decimal points placed in this region of densities. On the mapline the c designates that the c crystallographic axis is to go from page to page. The next 6 fields are the minimum and maximum fractional coordinates of the map which is to be generated 0 to .25 along a; 0 to 1 along b, and 0 to .25 along c.

FOURR fobs 
print *2 100.
grid 12 12 12
layout down across layer 13 13 13 0 0 0 1 1 1

In this case, it is desired to control the actual grid of the Fourier map scaled to 100 electrons per Angstrom cubed. A grid line is used to force twelfths along all axial directions. The layout line specifies the number of points to be calculated, the starting point, and the step or increment along all of the axial directions. The BL method is specified so that 13 points can be printed in every direction and if maximum h, k, or l should be greater than 12 the computation will still be done. Finally, the summation order is specified as c first - page to page, a second - down the pages, and b third - across the pages. This method of use can be very useful for checking that the map has the expected symmetry. This example, in fact, is a most useful check since twelfths or twenty-fourths will be divisible by the fractions of all symmetry operations. It is always a useful exercise to check to see that the points for a general position of the space group are all the same to within rounding. If it is determined that the space group symmetry is violated it is probably because systematically absent reflections have been entered in the bdf as if they were observed.

FOURR fobs ffsum
maxhkl 62 45 30
grid 126 96 64
layout layer down across 32 96 64 0 0 0 1 1 1

The compound used in this example is cytochrome c peroxidase. The crystal belongs to space group P2 2 2 with cell dimensions of 107A, 77A, and 51A. For a cell this large the preferred algorithm is FFT. In order to obtain a map with the asymmetric portion of the cell, the limits may be set in either one of two ways:

In either case, only 1/4 of the total map is calculated. However, the second case is preferable for two reasons: It induces calculation of fewer points along the largest axis and it takes advantage of the fact that the FFT will necessarily produce all of the coefficients for the points from 0 to 1 along y and z whether they are requested or not. The layout line therefore specifies that only 32 points should be calculated in the x-direction. Since there are to be 126 grid points between 0 and 1 along x, this will give the desired result.