An idealized set of coordinates must be supplied for
the rigid group to be placed in logical record
lratom:
of the bdf. Typically the rigid group will be
molecular fragments with no permitted internal rotations,
e.g. phenyl rings. There is no check made on the group
presented so the user may give any set of coordinates
desired.
Coordinates of atoms may be presented for calculation
either as fractional coordinates or orthogonal Angstrom
coordinates. The latter are useful when the rigid group is
calculated by hand from a model. The former may be altered
by hand from the coordinates obtained from a Fourier map or
from use of another program such as
BONDAT
. Whichever source is used for the ideal group, it
is necessary to specify how some atoms of the ideal group
are related to atoms of the "rough" or "natural" structure
as far as it is known.
The atoms used in the calculation will fall into two
subgroups; real and ideal. The real atoms are atoms of the
partially or fully solved structure while the ideal atoms
are atoms of the idealized group. The coordinates of the
atoms of both subgroups must be in the same region of the
unit cell and must be converging toward a connected set.
The term "connected set" is defined in the
BONDLA
program. Provisions have been made for modifying
coordinates of atoms in a partially or fully solved
structure to assure that this condition is met. The program
BONDLA will search a set of atoms for a connected
asymmetric set. If the idealized group lies in a special
position in the unit cell so that some of the atoms will be
related by a symmetry operation, provision has been made to
specify that this condition exists for the appropriate
atoms.
An approximate fit of the ideal group to the real
group is obtained by using the following formulae.
Orthogonal coordinates (matrix notation):
x' =
A x
where
A is the matrix to
transform fractional coordinates to orthogonal
coordinates (
lrcell:
, packet 4; relative to orthogonal axes a*,
b', and c);
x' are the orthogonal
coordinates; and
x are the fractional
coordinates.
Matrices for group-based unitary systems EI(ideal)
and ER(real):
-
The first 3 atoms will be used; they must not
be co-linear.
-
u is vector from
atom 1 to atom 2
-
v is vector from
atom 1 to atom 3
-
w is perpendicular
to
u and
v (
u ×
v )
-
E1 =
u (normalized)
-
E2 =
w ×
u (normalized)
-
E3 =
w (normalized)
Both systems are normalized.
Rotation matrix (ideal to real system)
R =
ER
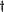EI
where
R is the rotation matrix
and
ER
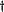is the transpose of
ER.
The idealized coordinates
x' (idealized) =
R x' (ideal)+
x' (atom 1)
The idealized coordinates are shifted so that the
sum of the x, y, and z derivatives between idealized and
real atoms is zero.
The idealized fractional coordinates
x (idealized) =
A
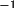x' (idealized)
where
A
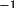= matrix to transform orthogonal coordinates to
fractional coordinates (record
lrcell:
, packet 5)
The atoms of the
real subgroup are loaded from the
archive bdf. When groups of atoms are in special
positions, pseudo-atoms may be added to the real subgroup
by means of
atomsy input lines.
These atoms are used to get the proper orientation of the
rigid group.
The atoms of the
ideal subgroup must be loaded from
input lines. Ideal atoms loaded as
atomor lines have
orthogonal Angstrom coordinates referred to an arbitrary
origin. Ideal atoms may also be supplied as fractional
coordinates on
atomfr input lines. A
cellid line must
precede the
atomfr lines and
contain the unit cell parameters which define the
atomfr coordinates. The
origin is again arbitrary.
The correspondence between atoms in the two
subgroups is established through the labels of atom sites
from the bdf,
atomsy,
atomor, and/or
atomfr input lines. Any
atoms in the ideal subgroup not identified with ones in
the real subgroup are assumed to be undetermined. These
atoms will be appended to the real subgroup at the end of
the fitting process if
atname lines have been
supplied to establish atom labels in the real
subgroup.
If a structure possesses many copies of the
idealized group, it may be replicated as many times as
required in various locations in the unit cell by use of
atname input lines.
These lines allow the renaming of atoms in the idealized
subgroup so they will match others in the real subgroup.
The number of atoms specified in
atname lines must, in
each instance, be the same as the number of members in
the ideal subgroup.
The
rigid line permits the
establishment of an isotropic thermal displacement
parameter, population parameter, and multiplicity factor
for the members of the generated group(s). This program
has been adapted from the RIGBOD program of XRAY76 which
was written by N.W. Alcock and adapted by Schwaba
(1976).
Two phenyl groups are generated, the first one
fitting atoms
C1to
C6, the
second one fitting atoms
C11to
C16. Real
atoms are read from the bdf and lines with fractional
coordinates are written to the punch file.
