SORTRF : Sort/merge reflection data

This site uses JavaScript, but it seems to be unavailable.Some functionality may therefore be broken.AccessKeysHomeDocRootStartPrevDocNextDocUpPrevNextTopBottom

`SORTRF` : Sort/merge reflection data

Authors: Syd Hall, Nick Spadaccini and Jim Stewart

Contact: Syd Hall, Crystallography Centre, University of Western Australia, Nedlands 6907, Australia.

SORTRF sorts and, optionally, averages the reflection data on an archive bdf.

Method

SORTRF applies two important processes to reflection data on the bdf. Reflections may be sorted by their Miller indices so that they are in an order that is optimal for subsequent calculations. According to the sort algorithm selected reflections which are symmetrically equivalent may be placed together or treated independently. This is detailed in the next section. The second function of SORTRF is to average reflection data which are symmetrically equivalent. That is, multiple observations of reflections and their Friedel mates are reduced to a single packet with an averaged value stored for the reflection. The averaged values for the Friedel related reflection $^{1}$ may be treated and stored independently if requested.

1 Note that SORTRF should be applied before ADDREF if the intensity data, rather than the Frel data, is to be averaged. Note also that systematically absent data are not removed by SORTRF - this is done in ADDREF.

Sorting Reflection Data

The sort order of reflections is the measure that each Miller index changes from reflection to reflection. The input option order smf on the SORTRF line determines the sort order. The parameter smf is the combination of characters h, k, and l. s designates the slowest varying index; f designates the fastest varying index. Thus the entry of order khlspecifies that kwill be slowest varying and lfastest varying.

Three sort algorithms are available for the treatment of equivalent reflections. These are referred to as sort types.

Sort type 1: Sort only mode

In this mode data is sorted so that each index, within the constraints of the specified sort order, will start with its most negative index and finish with its most positive index. No account will be taken of symmetry equivalent reflections and no transformation of the input indeices will take place. This is strictly a sort only mode. This is the default provided aver or clus options are not set.

Sort type 2: adjacent Friedel mode

This sort type is identical to 1 except that the Miller indices of equivalent reflections are transformed to have matching (and most positive) values. If the pakfrl or sepfrl flags are entered then the Friedel equivalent reflections will be treated independently and will be immediately adjacent in the sort list. If the flags pakfrl or sepfrl are not entered the Friedel related data will be treated identically to symmetrically equivalent data. This is the default mode if the aver or clus options are set.

Sort type 3: group magnitudes mode

This sort type is identical to 1 except that the Miller indices of equivalent reflections are transformed to have matching (and most positive) values. In addition all reflections with the the same index magnitudes are adjacent in the sort list (note that reflections with matching index magnitudes are not necessarily symmetrically equivalent). The treatment of Friedel data is identical to a type 2 sort. This mode is intended for speeding up a Fourier calculation which uses the Beevers-Lipson algorithm. It is not suitable for listing purposes and it is not recommended except for very large data sets on a relatively slow computer.

Averaging Reflection Data

In addition to sorting data, SORTRF may be used to average or cluster multiple observations and symmetrically equivalent reflection data. The SORTRF options for this are noav, aver and clus. noav is the default and specifies that no averaging of equivalent data will take place. clus causes equivalent reflections with there original untransformed indices to be adjacent in the sorted list and that no averaging take place.

aver will cause the specified coefficients (Frel, 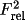$F^{2}_{\rm{rel}}$ or Irel) of equivalent reflections to averaged. If not specified the averaged coefficient is assumed first to be Irel; if these data are not present Frel will be averaged. Note that only the specified coefficients are averaged; other coefficients are not averaged. The two averaging processes available in SORTRF are described below.

`aver 1`: standard average with culling

This algorithm provides for a standard average to be calculated, with the provision for culling data which exceeds a certain deviation from the initial mean. In the following treatment, the intensity I may be replaced by | 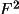$F^{2}$ | or |F| according to what is specified on the SORTRFline. The initial mean intensity is calculated as:

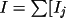$I = \sum [I_{j}$ ] / N where N is the number of equivalents.

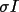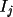The $\sigma I$ is calculated from the individual $I_{j}$ e.s.d.'s (estimated usually from counting statistics), plus the deviations of the contributing intensities from the initial mean. That is,

$\sigma I = max((\sum I_{j})^{1/2}/N, [N\sum I_{j}^{2}-(\sum I_{j})^{2}/(N(N-1))]^{1/2}, 0.0001)$

If the cull t option is specified any individual intensity that deviated from the initial mean by greater than t $\sigma$ I is culled before the final mean I is calculated.

`aver 2`: Fisher Test

The second averaging process consists of finding the arithmetic average of reflection intensity is:

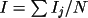$I = \sum I_{j}/ N$ where N is the number of equivalents.

Two measures are made of the variance of the average intensity I. One is based on Poisson statistics, and the other is based on the scatter of equivalents,

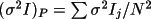
$(\sigma ^{2}I)_{P}= \sum \sigma ^{2}I_{j}/ N^{2}$

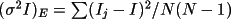
$(\sigma ^{2}I )_{E}= \sum (I_{j}-I)^{2}/ {N(N-1)}$

Since both measures have different degrees of freedom, N and N-1 respectively, a test can be made for the hypothesis that they are equal to the 1 significance level of the Fisher distribution. This is referred to as the Fisher test (Hamilton, 1964). Reflections whose measures of variance prove equal (the hypothesis is successful) may have the adjusted $\sigma$ I for the average intensity optionally set to one of the following values by the success option:

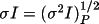
i. $\sigma I = (\sigma ^{2}I )_{P}^{1/2}$

ii. $\sigma I = (\sigma ^{2}I )_{E}^{1/2}$

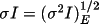
iii. $\sigma I = max(i,ii)$

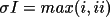
Reflections whose measures of variance prove unequal (the hypothesis is unsuccessful) may have the adjusted σI for the average intensity optionally set to the above, or rejected (rcode=2, σI= voidflg: ) by the unsuccess option on the SORTRF line.

Note that this option will assign an rcode of 2 to a reflection if, and only if, the tests fail to satisfy the hypothesis relating to its variances and if this is explicitly requested by the user in the unsuccess option. All reflections which satisfy the hypothesis will have an rcode of 1.

Agreement Factors

Two agreement factors are provided to measure the quality of the averaged data:

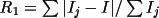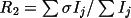$R_{1}= \sum |I_{j}- I | / \sum I_{j}$ and $R_{2}= \sum \sigma I_{j}/ \sum I_{j}$ .

Treatment Of Friedel Pairs

Attention must be drawn to the necessity of calculating a |Frel| corrected for the effects of dispersion prior to use in an electron density calculation with FOURR . The dispersion corrections to |Frel| for reflection and anti-reflection are not equal. With Friedel data packed into the same packet of the bdf, as is necessary for absolute structure refinement, a dispersion-free |Frel| can be correctly calculated from the |Frel|'s for the reflection and anti-reflection with CRYLSQ . However, this is only possible if the |Frel|'s of Friedel pairs are not averaged! The average |Frel| is made up of (weighted) contributions from m reflections and n anti-reflections. The weights and the values of m and n vary from one reflection to another, and a proper calculation of the dispersion correction to |Frel| needs to know all of these values. It means that electron density calculations made with packed pairs, and from averaged pairs will almost certainly differ. The electron density calculated from the packed data is correct.

Friedel related reflections will be treated as symmetrically equivalent data unless either the pakfrl or sepfrl options are entered. If these options are specified Friedel pairs are are treated as independent data and are not averaged. If pakfrl is entered the Friedel data is placed in the same lrrefl: packet on the bdf.

The packed Friedel data is needed if absolute structure parameters are to be refined by CRYLSQ.

If the sepfrl option is used the Friedel pair data is stored in separate but adjacent lrrefl: packets.

Note that invocation of either option will automatically cause the data to be averaged. If no aver option is stated then mode 1 is assumed.

File Assignments

Reads reflection data from the input archive bdf
Writes sorted and/or averaged data to the output archive bdf

Examples

SORTRF order lkh

Data will be sortedwith h changing most rapidly, and k next most rapidly.

SORTRF aver 1 cull 2.5 print 512

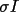During averaging measurements >2.5 $\sigma I$ from the initial mean are culled and a new average computed. The first 512 reflections will be printed.

SORTRF aver 2 succe 3 unsuc 4 print -9999

This example uses the Fisher average. Those reflections satisfying the hypothesis will have σI based on the maximum variance. Those reflections failing to satisfy the hypothesis will be rejected. The first 9999 reflections which fail to satisfy the hypothesis are printed.