PARTN
: Hirshfield partitioning
Author: Nick Spadaccini,
Computer Science Department, University of Western Australia,
Nedlands 6907, Australia
PARTN partitions an input density into either the
contribution of a particular atom (
fragment
) or of an atom and its symmetry equivalents
(
entire
). The Hirshfeld method of partitioning is
employed.
The Hirshfeld (1977) method apportions the electron
density among the atoms by the appropriate weighting. The
weights are related by the atomic contribution to the
promolecular density
|
(4.79) |
![\[
w_{A}(\Vector{r}) = \frac{\rho_{\rm{atm}}^A(\Vector{r})} { \rho_{\rm{pro}}(\Vector{r})}
\]](equations/4.43.1-eq-79.gif) |
The fragment of the density apportioned to atom A
is
|
(4.80) |
![\[
\rho_{\rm{frag}}^A(\Vector{r}) = w_{A}(\Vector{r})
\rho_{\rm{mol}}(\Vector{r})
\]](equations/4.43.1-eq-80.gif) |
An alternative scheme is based on the atomic
contributions to the total promolecular potential
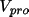defined as the sum of
the electronic and nuclear contributions.
Density And Potential Profiles
The promolecular density or potential is the sum of
the atomic densities or potentials. These latter values are
derived from the Clementi and Roetti (1974) atomic
wavefunctions. Associated with each atom type are the
parameters
,
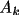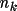and
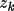for k=1, ... , m such that
the density is
|
(4.81) |
![\[
\rho_{\rm{atm}}(\Vector{r}) =\sum_{k=1}^{m}{ A_k r^{n_k}e^{-z_k r} }
\]](equations/4.43.2-eq-81.gif) |
and the potential is
|
(4.82) |
![\[
V_{\rm{atm}}(\Vector{r}) =4\pi \sum_{k=1}^{m}{ A_k \left(
\frac{\gamma(n_k+3,z_k r) }{r z_{k}^{n_k+3} } +
\frac{(n+1)! }{ z_{k}^{n_k+2} } -
\frac{\gamma(n_k+2,z_k r) }{ z_{k}^{n_k+2} } \right)
+ \frac{Z_A}{r} }
\]](equations/4.43.2-eq-82.gif) |
The last term is the nuclear contribution and
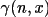is the
Incomplete Gamma Function.
The density profiles (
) and potential
profiles (e/bohr) are stored at 44 discrete values of r
(bohrs) for the points,
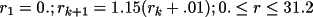
The divisions are chosen so that the density of
points is greatest in the region of steepest gradient. The
density or potential value at any general point is linearly
interpolated from the profile.
The structural data is read from the input archive
bdf. The density must be input on file
map. PARTN partitions
this density into the atomic contributions. The density
ascribed to the fragment atom or the entire atom specified
on the
site line is output to
file
par.
The user may specify the effective range of atom
contributions in two ways. The
border
option in the program initiation line
determines the region beyond the input map for which atom
contributions are included. The default value of 6Ĺ
implies that any atom within this distance of the input map
edges is included. The distance beyond which an atom
contribution is zero may also be set by the
contact
option.
-
Reads atom data from the input archive
bdf
-
Reads density map from the file
map
-
Reads
profdbdata base from a file defined by the
macro
profile:
-
Writes partitioned density map to the file
par
This example employs all the default settings. The
weights are determined from the promolecular density. The
contributions of atoms up to 6Ĺ beyond the input
map edges are included in the calculation. However, an atom
will not contribute to the density if the point is greater
than 6Ĺ away. The partitioned density will include
the contribution of the
O12atom at
(.1234,-.1234,.7890) only.
Here the weights are determined from the promolecular
potential. Atoms up to 4Ĺ from the input map edges
are included in the calculation. The effective range of an
atom is set to 4.5Ĺ. The partition density will
include the contributions of all the
Cu1abatoms in
the input range.
-
Clementi, E. & Roetti, C. 1974.
Atomic Data and Nuclear Data
Tables.
14, 177-478.
-
Hirshfeld, F. 1977.
Israel Journal of Chemistry.
16,198-201.
